arfa's musings about a coin spinning on a tabletop
- Thread starter arfa brane
- Start date
I'm good.
p.s. I already know what a classical Hamiltonian for a system in SHM looks like. I don't like cheating though.
p.s. I already know what a classical Hamiltonian for a system in SHM looks like. I don't like cheating though.
From Wikipedia, a diagram of a spinning top labelled with force vectors.
It doesn't label the frictional component, which as assumed, is what damps the frequency $$ \omega_s$$.
The upwards force $$ -F_g$$, is "reactive"; the surface the top is moving along as its angular momentum (vector L) precesses "around" the axis of rotation with frequency $$ \omega_p$$, is generating an elastic force. That is, the surface of a table reacts elastically, like a spring, so we just write
$$F_g = -kx$$; this does not give x in terms of precessional motion and torque. The restoring (elastic) force would be there if there was no torque, it's a general property of oscillating systems. It's easier when the oscillations are of a weight attached to a spring, in which case x is the position of the weight (or of its centre of mass).
A general equation for SHM is : $$ m \frac {d^2} {dt^2} + kx = 0$$, for undamped oscillations.
. . .
It doesn't label the frictional component, which as assumed, is what damps the frequency $$ \omega_s$$.
The upwards force $$ -F_g$$, is "reactive"; the surface the top is moving along as its angular momentum (vector L) precesses "around" the axis of rotation with frequency $$ \omega_p$$, is generating an elastic force. That is, the surface of a table reacts elastically, like a spring, so we just write
$$F_g = -kx$$; this does not give x in terms of precessional motion and torque. The restoring (elastic) force would be there if there was no torque, it's a general property of oscillating systems. It's easier when the oscillations are of a weight attached to a spring, in which case x is the position of the weight (or of its centre of mass).
A general equation for SHM is : $$ m \frac {d^2} {dt^2} + kx = 0$$, for undamped oscillations.
. . .
What I was trying to do here was look at the frictional component of a spinning coin, and determine how friction is responsible for slowing the frequency and tipping the coin over (at a critical point, say).
Given that the physics applies to a coin with no faces (or with two heads, say), I need to abstract the physics so a "choice" is made.
But since I can just look it all up and figure it out, all by myself, without posting a damn thing, and since I'm the only one who gives a damn, that's actually what I did. I was just trying to follow some kind of logical progression, but I know, in general most people haven't got the patience, probably that's why James R decided to send me to Coventry.
But I haven't got the time to dick around with that. Wait, what the hell am I saying . . .?
Oh yeah, who cares . . . ha ha. Besides I have a car that needs a bit of repair, and somehow this lone, individual effort, without any input from an audience, is way more satisfying.
Or I could pick up my guitar and play. Guitar strings (did you know?) are also oscillating systems when you pluck or strum them; my rasguedo needs a bit of work though I have to say.
Physics? Who said anything about physics?
No physics here mate, just me guitar. /Liverpool_accent
Given that the physics applies to a coin with no faces (or with two heads, say), I need to abstract the physics so a "choice" is made.
But since I can just look it all up and figure it out, all by myself, without posting a damn thing, and since I'm the only one who gives a damn, that's actually what I did. I was just trying to follow some kind of logical progression, but I know, in general most people haven't got the patience, probably that's why James R decided to send me to Coventry.
But I haven't got the time to dick around with that. Wait, what the hell am I saying . . .?
Oh yeah, who cares . . . ha ha. Besides I have a car that needs a bit of repair, and somehow this lone, individual effort, without any input from an audience, is way more satisfying.
Or I could pick up my guitar and play. Guitar strings (did you know?) are also oscillating systems when you pluck or strum them; my rasguedo needs a bit of work though I have to say.
Physics? Who said anything about physics?
No physics here mate, just me guitar. /Liverpool_accent
Last edited:
No, wait, I think I've spotted a pattern here; one that another sometime moderator has spotted, but who tends to couch their criticism in somewhat Shakespearian language.
Which is that, James is after a perticular version of "how to do science"; an idol, or an icon of sorts.
I haven't trotted out enough physics in enough time, clearly, to live up to his version of prospecting for my science patch.
So, complaints aside, thankyou James, for furthuring my education in human nature; I am, after all, an armchair anthropologist, I'm interested in what drives people to aspire to, whatever it is people think they are aspiring to; I don't sit here and ask myself, why am I bothering.
But I can just sit here and not bother posting anything; if that will help.
Cheers.
p.s. yes, I know why I'm here, thanks; how about you?
Which is that, James is after a perticular version of "how to do science"; an idol, or an icon of sorts.
I haven't trotted out enough physics in enough time, clearly, to live up to his version of prospecting for my science patch.
So, complaints aside, thankyou James, for furthuring my education in human nature; I am, after all, an armchair anthropologist, I'm interested in what drives people to aspire to, whatever it is people think they are aspiring to; I don't sit here and ask myself, why am I bothering.
But I can just sit here and not bother posting anything; if that will help.
Cheers.
p.s. yes, I know why I'm here, thanks; how about you?
No, fuck it, as John Lennon said.
The question is, why plug in a frictional component, and call it the resistance of a forced oscillator? Once you have this thing called resistance (classical SHM resistance has units of $$kg.s^{-1}$$, for a damped velocity, angular or rectilinear).
Why formulate a Hamiltonian and call it a measurement operator . . .
James? . . . . James, can you explain why someone, anyone will do, would bother with this?
The question is, why plug in a frictional component, and call it the resistance of a forced oscillator? Once you have this thing called resistance (classical SHM resistance has units of $$kg.s^{-1}$$, for a damped velocity, angular or rectilinear).
Why formulate a Hamiltonian and call it a measurement operator . . .
James? . . . . James, can you explain why someone, anyone will do, would bother with this?
This thread is now quite likely, about James R's musings on why someone would muse upon a simple example of a physical system, and claim they can use the physics to explain what probability is when you make it functional.
The principle of least action in physics is, roughly speaking, that a particle in motion will try to minimise the difference between its kinetic and potential energies. Lagrangian mechanics (and Hamiltonian mechanics) both depend on this principle; Lagrangians have generalised positions and velocities, Hamiltonians have generalised momenta.
Indeed these are both applicable to electronic circuits; the Kirchoff relations between voltages and currents can be expressed as an Euler-Lagrange equation of motion. A classical electronic current is treated like an electric fluid (an electron gas, if you will). The symmetries are expressed in the conservation of charge (KVL). It helps if you can see the connection between free and forced oscillations in Newtonian mechanics and the same phenomena in RLC circuits.
The caveat with resistance (viscosity, friction, . . .) is that it is a dissipative "force", it isn't conservative because heat is generated and lost to the environment.
The classical Hamiltonian for SHM (such as for a rigid or a spring pendulum) includes the frictional coefficient, but you can't consider it outside of the other forces acting on the system.
Are we getting the hint?
The principle of least action in physics is, roughly speaking, that a particle in motion will try to minimise the difference between its kinetic and potential energies. Lagrangian mechanics (and Hamiltonian mechanics) both depend on this principle; Lagrangians have generalised positions and velocities, Hamiltonians have generalised momenta.
Indeed these are both applicable to electronic circuits; the Kirchoff relations between voltages and currents can be expressed as an Euler-Lagrange equation of motion. A classical electronic current is treated like an electric fluid (an electron gas, if you will). The symmetries are expressed in the conservation of charge (KVL). It helps if you can see the connection between free and forced oscillations in Newtonian mechanics and the same phenomena in RLC circuits.
The caveat with resistance (viscosity, friction, . . .) is that it is a dissipative "force", it isn't conservative because heat is generated and lost to the environment.
The classical Hamiltonian for SHM (such as for a rigid or a spring pendulum) includes the frictional coefficient, but you can't consider it outside of the other forces acting on the system.
Are we getting the hint?
Right. Friction.
The reason a pointy top is a good example of how to use generalised 'coordinates'; you can for instance set up some unit vectors, parallel to the axis of rotation, then you have an angle, $$ \phi$$, the angle this axis makes with the vertical, so also the horizontal. It changes with time, you observe drily.
So you also have $$ \frac {d} {dt} \phi$$. The nice thing about the precessing top is the friction is low, it should spin for quite a while on say, a flat polished glassy surface; So it will trace out quite a long path on this surface if it experiences torque.
But a coin isn't like that, it has a goldilocks amount of friction on a wooden polished table top, even if you give it quite a lot of initial momentum; doing this by holding back a finger with your thumb, then building up a bit of tension and letting go suddenly means the coin sees a sudden impulse (there is an input waveform, like an upside down U).
The idea then is the frictional interaction is constrained; likewise for a coin or a pebble in free fall in a viscous fluid, the interaction is constrained by surface areas. Friction looks like it can be used to measure, i.e. prepare a known state, in a physical system.
Just sayin'
Oh yeah, that finger-thumb thing is an elastic forcing, it follows that the transfer of momentum is an elastic function (in the good old time domain). This also follows from the observation that all surfaces are elastic.
The reason a pointy top is a good example of how to use generalised 'coordinates'; you can for instance set up some unit vectors, parallel to the axis of rotation, then you have an angle, $$ \phi$$, the angle this axis makes with the vertical, so also the horizontal. It changes with time, you observe drily.
So you also have $$ \frac {d} {dt} \phi$$. The nice thing about the precessing top is the friction is low, it should spin for quite a while on say, a flat polished glassy surface; So it will trace out quite a long path on this surface if it experiences torque.
But a coin isn't like that, it has a goldilocks amount of friction on a wooden polished table top, even if you give it quite a lot of initial momentum; doing this by holding back a finger with your thumb, then building up a bit of tension and letting go suddenly means the coin sees a sudden impulse (there is an input waveform, like an upside down U).
The idea then is the frictional interaction is constrained; likewise for a coin or a pebble in free fall in a viscous fluid, the interaction is constrained by surface areas. Friction looks like it can be used to measure, i.e. prepare a known state, in a physical system.
Just sayin'
Oh yeah, that finger-thumb thing is an elastic forcing, it follows that the transfer of momentum is an elastic function (in the good old time domain). This also follows from the observation that all surfaces are elastic.
Last edited:
I know, I know, who studies this shit?
There's a whole paper on google scholar devoted to what happens when a spinning coin stops spinning, you know, like a top, and tips over.
This might be analogous to what electronics engineers call a ringdown.
Anyway, the author develops a model in which a disk oscillates on its edge, in a rolling motion, forever. Then introduces a dissipative term that damps the motion. In this oscillatory mode the relations between all the forces are a bit different.
Physics recall, has to include all the macroscopic stuff, then try to make the microscopic stuff look the same but clearly it, namely friction, is not macroscopic, it almost needs its own Hamiltonian, or it needs to be pinned to a set of dependencies.
But it's always going to introduce some noise, it's why a coin wanders around but generally curves in the same direction as the spin. Its angular momentum dominates initially, but the microscopic "Hamiltonian" is a random walk.
Abstract
It is a fact of common experience that if a circular disk (for example, a penny) is spun upon a table, then ultimately it comes to rest quite abruptly, the final stage of motion being characterized by a shudder and a whirring sound of rapidly increasing frequency. As the disk rolls on its rim, the point P of rolling contact describes a circle with angular velocity Ω. In the classical (non-dissipative) theory1, Ω is constant and the motion persists forever, in stark conflict with observation. Here I show that viscous dissipation in the thin layer of air between the disk and the table is sufficient to account for the observed abruptness of the settling process, during which, paradoxically, Ω increases without limit. I analyse the nature of this ‘finite-time singularity’, and show how it must be resolved.
https://www.nature.com/articles/35009017
There's a whole paper on google scholar devoted to what happens when a spinning coin stops spinning, you know, like a top, and tips over.
This might be analogous to what electronics engineers call a ringdown.
Anyway, the author develops a model in which a disk oscillates on its edge, in a rolling motion, forever. Then introduces a dissipative term that damps the motion. In this oscillatory mode the relations between all the forces are a bit different.
Physics recall, has to include all the macroscopic stuff, then try to make the microscopic stuff look the same but clearly it, namely friction, is not macroscopic, it almost needs its own Hamiltonian, or it needs to be pinned to a set of dependencies.
But it's always going to introduce some noise, it's why a coin wanders around but generally curves in the same direction as the spin. Its angular momentum dominates initially, but the microscopic "Hamiltonian" is a random walk.
Abstract
It is a fact of common experience that if a circular disk (for example, a penny) is spun upon a table, then ultimately it comes to rest quite abruptly, the final stage of motion being characterized by a shudder and a whirring sound of rapidly increasing frequency. As the disk rolls on its rim, the point P of rolling contact describes a circle with angular velocity Ω. In the classical (non-dissipative) theory1, Ω is constant and the motion persists forever, in stark conflict with observation. Here I show that viscous dissipation in the thin layer of air between the disk and the table is sufficient to account for the observed abruptness of the settling process, during which, paradoxically, Ω increases without limit. I analyse the nature of this ‘finite-time singularity’, and show how it must be resolved.
https://www.nature.com/articles/35009017
Ah you see what you're supposed to do to kick a Hamiltonian into action and make what you then claim is a measurement of a physical state (!)
You look at say, all the forces acting, in an initial condition where the microscopic d.o.f. are suppressed. With a coin or metal disk with thickness h sitting on edge in a 'stationary condition', the restoring force is directed from the line across the coin of length h, upwards through the center of mass.
All the stress the weight of the coin produces along the line of contact is distributed over a linear density with units $$ kg.m^{-1}$$.
When the coin rotates around a rotation axis, this line of matter is where all the friction occurs, the coin scrapes its way around the tabletop tracing out an area. It also has to push air molecules away, but that can be suppressed by having a vacuum instead, then only the two interacting surfaces are generating the "noisy part".
So that's one constraint. The frictional contribution is bounded.
You look at say, all the forces acting, in an initial condition where the microscopic d.o.f. are suppressed. With a coin or metal disk with thickness h sitting on edge in a 'stationary condition', the restoring force is directed from the line across the coin of length h, upwards through the center of mass.
All the stress the weight of the coin produces along the line of contact is distributed over a linear density with units $$ kg.m^{-1}$$.
When the coin rotates around a rotation axis, this line of matter is where all the friction occurs, the coin scrapes its way around the tabletop tracing out an area. It also has to push air molecules away, but that can be suppressed by having a vacuum instead, then only the two interacting surfaces are generating the "noisy part".
So that's one constraint. The frictional contribution is bounded.
I just realised I can prove the above with a thought experiment, in a vacuum.
Have a not-too-smooth surface which is flat with a spring constant as usual, and cover it with a fine layer of dust which is a different color.
So a coin 'scraping' along the surface, by precessing on its rim and one or the other edge, will leave a track behind, a path in this dust, without damping the system too much.
Now the product $$ \lambda \nu $$, with units of Newtons, makes a little more sense--the $$\lambda $$ term has those $$kg.s^{-1}$$, in the microscopic interaction--where the spinning coin displaces the dust you have a minimal amount of energy writing--something.
Have a not-too-smooth surface which is flat with a spring constant as usual, and cover it with a fine layer of dust which is a different color.
So a coin 'scraping' along the surface, by precessing on its rim and one or the other edge, will leave a track behind, a path in this dust, without damping the system too much.
Now the product $$ \lambda \nu $$, with units of Newtons, makes a little more sense--the $$\lambda $$ term has those $$kg.s^{-1}$$, in the microscopic interaction--where the spinning coin displaces the dust you have a minimal amount of energy writing--something.
Last edited:
Prior to this post, I made exactly 4 posts to this thread. Here is a summary of their content:
1. (Post #2) I offered up an answer to the question you put in the opening post.
2. (Post #17) I commented, after a succession of further posts from you that attracted no responses from anybody, that you seemed to be talking to yourself.
3. (Post #18) I made a one-line post about an error I thought I saw in one of your posts.
4. (Post #21) I realised that it was my error, not yours, and I apologised for my inapplicable post #18.
That is the entire extent of my recorded "musings" on this topic.
I don't quite understand why you're fixated on what I might think about your string of posts. You may get more responses if you try addressing your thoughts to the entire forum, rather than demanding my undivided attention.
Of course, posting something other your current stream-of-consciousness internal monologue might also help in that regard. Something to consider.
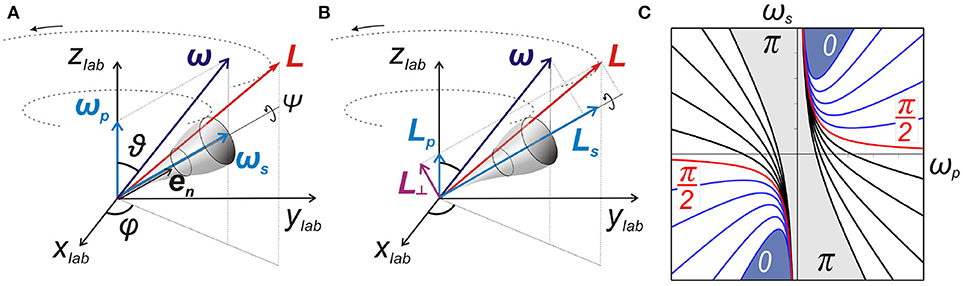
Don't you love diagrams that explain themselves with as little as needed?
What the first two are about, is the vectors lying in the same plane in either case. In A, the angular frequency $$ \omega$$ of the precession is the sum $$ \omega_p + \omega_s$$. In B $$ L = L_p + L_s $$. So we have an angular basis, and a momentum basis. In B you have this extra $$ L_{\bot} $$ is perpendicular to $$ L_s $$.
So these alternate frames are corotating with the precession, all coplanar.
C is a plot of various smoothly varying values for the colors used in A and B, and how the two angular moments are related. It's a plot of the function $$ f(\omega) = \omega_p + \omega_s$$
No. The angular frequency of precession is just $$\omega_p$$
In A, the angular frequency $$ \omega$$ of the precession is the sum $$ \omega_p + \omega_s$$.
How does your second statement follow from your first?
Extra? What do you mean?
Which alternate frames? Alternate to what?
What exactly is plotted there? The axes are clearly labelled, but what are the curves? Explain.
Why is that useful?
Why can you see a symmetry in the plot?
You're coming across like a 5 year old. Grow the fuck up.
For fuck's sake, you now want me to trot stuff out for the grade schoolers? Look, the colors in C explain themselves, once you've taken the time to notice A and B also have colors in them.
Yes you're right there is one angular precession vector; but gee, look what happens when you add the angular velocity of the top to it, you get another vector in the same plane! Gee, so what?
I thought you might know about that stuff, but your questions indicate a level of naivete I can't gauge properly.
For fuck's sake, you now want me to trot stuff out for the grade schoolers? Look, the colors in C explain themselves, once you've taken the time to notice A and B also have colors in them.
Yes you're right there is one angular precession vector; but gee, look what happens when you add the angular velocity of the top to it, you get another vector in the same plane! Gee, so what?
I thought you might know about that stuff, but your questions indicate a level of naivete I can't gauge properly.
Last edited:
Did I say something about symmetry? (???)
You don't like people asking questions? Or you just don't like me asking questions?
I didn't ask about the colours.
Another question: what do the notations $$\pi$$ and $$\pi/2$$ relate to in that plot?
When you add any two vectors, you'll always get a vector sum that is in the plane defined by the two vectors you're adding (assuming non-parallel vectors, which define a unique plane).
That's what I'm asking you.
So, James, are you admitting you're trying to test my knowledge of the physics of a precessing top?
Or that, in a nutshell, I can explain what the plot in C is explaining about the diagrams in A and B, say. Like an IQ test of sorts.
Y'know, how good am I at spatial reasoning, or abstracting ideas like addition, stuff like that?
Or, do I have a well-developed sense of color? What is it, I wonder?
°
Alrighty; I shall play the following card. The labels $$ \pi$$ and $$ \pi / 2$$, notice, are black and red, respectively. These label each axis.
And again, so what.
Ok, what the hell. In each of A and B, all the colored vectors precess at the same rate as $$ \omega_p$$. So any vector corotating with $$ \omega_p$$, so all those coplanar to L, has the same angular frequency.
Or that, in a nutshell, I can explain what the plot in C is explaining about the diagrams in A and B, say. Like an IQ test of sorts.
Y'know, how good am I at spatial reasoning, or abstracting ideas like addition, stuff like that?
Or, do I have a well-developed sense of color? What is it, I wonder?
°
Alrighty; I shall play the following card. The labels $$ \pi$$ and $$ \pi / 2$$, notice, are black and red, respectively. These label each axis.
And again, so what.
Ok, what the hell. In each of A and B, all the colored vectors precess at the same rate as $$ \omega_p$$. So any vector corotating with $$ \omega_p$$, so all those coplanar to L, has the same angular frequency.
Last edited:
I was trying to work out what the point of this thread is supposed to be.
You started off with one question. Then you moved onto some irrelevant stuff about simple harmonic oscillators. Then you went off on some tangent about anthropology. Then you mentioned forced oscillators and dropped the word "Hamiltonian" in a few times, more or less at random. Then you moved onto "elastic forcing", whatever that is. Then you cited a paper which probably answers your original question. Then you talked about measuring physical states. Then there was some rubbish about friction acting along a "line of matter". Then you said something about surface dust. Then something something about diagrams of the angular momentum of a precessing top, with a graph you can't seem to explain.
There was some other stuff in there that I've skipped over in this description.
To summarise, it seems like you're trying to put on some kind of show, in which you drop some physics terms into a thread in the hope that readers might assume that you're doing deep physics "behind the scenes", or in your head, or something. Perhaps you think they'll assume that - somewhere else - you're actually writing down some mathematics or equations and trying to solve a physics problem.
I don't understand what the point of your display is. And who exactly do you think you're fooling? And why is it important to try to fool people in that way?