Pinball1970
Valued Senior Member
A moment of clarity.
Not really. Biologists have known this for years.
Do you want to know about science or not?
A moment of clarity.
Not really. Biologists have known this for years.
Do you want to know about science or not?
That is not what mathematics is.What is it about mathematics (the symbolization of values) that makes it unsuitable to explain the universe?
Then tell me what it is before I forget 7 years of integrated accounting of 7 separate community improvement programs, recording all facets of spending on needed supplies and labor, accounting for all allotted capitalThat is not what mathematics is.
I can't possibly be that obtuse?Math is used extensively to explain aspects of the universe. I don't know what you mean by the "symbolization of values", but I don't think that matters.
A mathematical symbol can represent any relational value.A number is an arithmetic value used to represent quantity. Hence, a number is a mathematical concept used to count, measure, and label. Thus, numbers form the basis of mathematics.
Q: What is a property in math?In the previous section, we described periodic waves by their characteristics of wavelength, period, amplitude, and wave speed of the wave.
Waves can also be described by the motion of the particles of the medium through which the waves move. The position of particles of the medium can be mathematically modeled as wave functions, which can be used to find the position, velocity, and acceleration of the particles of the medium of the wave at any time. https://phys.libretexts.org
Q: What are mathematical functions?In mathematics, a property is a characteristic that always remains true. Number properties are at the core of mathematics and help us to understand and work with complex equations and problems. Certain properties will always hold true whether you're dealing with addition, multiplication, division or anything else.May 30, 2023. https://www.learner.com/blog/what-are-the-properties-of-math#
16.4.1 Neural network predicting AIMs
Neural networks are biologically inspired mathematical functions that have individual layers of nodes, each node in a layer being connected to every node in the subsequent layer with learned weighted connections and used to generate output values (of any dimension) based on input values (of any dimension). This last property was particularly important to this project, having 47 output values and 40 input values, because not all algorithms or structures of neural networks are as flexible.
The network used for AIM has 3 hidden layers, all of which are linear, with varying numbers of nodes in each layer. The objective of predicting the associated impact measures is fulfilled by training and deploying the model shown in Fig. 16.5. Referring to the pipeline in Fig. 16.2, the model is the endpoint of the AIM system backend and the starting point for the AIM system frontend, where new laws can be predicted upon to assist policy researchers and data scientists. https://www.sciencedirect.com/topics/mathematics/mathematical-function#
Ironically enough I don't know what you're referring to.I can't possibly be that obtuse?
You're gonna have to clarify that assertion. I'd like to know what mathematics are used for by humans, if not to label, codify, quantify, qualify, symbolize, and in general do science.It's not a label thing.
Playing chess is doing mathematics.Exploring what it means to know and do mathematics
▶WHAT DOES IT MEAN TO DO MATHEMATICS? Mathematics is more than completing sets of exercises or mimicking processes the teacher explains. Doing mathematics means generating strategies for solving a problem, applying that strategy and checking to see whether your answer makes sense. Finding and exploring regularity or order, and then making sense of it, is what doing mathematics in the real world is all about. https://www.pearson.com/en-au/media/2471366/9781488615627.pdf
Point made.Ironically enough I don't know what you're referring to.
No physical interactions involve mathematical functions. Mathematics is conceptual. Physics is ... physical.OK, then try to fashion a physical interaction that does not invoke a mathematical function.
Like what?Oh, Bohm had some wonderful insights.
Why did you ignore the question I asked you?What model can promise a TOE except a mathematical model.
You were wrong, again.Oh, I thought that all equations are self-referential.
There's no such thing as a "relational value". That's just something you made up.A: A mathematical symbol can represent any relational value.
That is incorrect.Neural networks are biologically inspired mathematical functions...
Right. Let me rephrase.That is incorrect.
In biology, homeostasis is the state of steady internal, physical, chemical, and social conditions maintained by living systems. This is the condition of optimal functioning for the organism and includes many variables, such as body temperature and fluid balance, being kept within certain pre-set limits. Other variables include the pH of extracellular fluid, the concentrations of sodium, potassium, and calcium...etc, etc, etc. Wikipedia
Abstract
According to medical guidelines, the distinction between “healthy” and “unhealthy” patients is commonly based on single, discrete values taken at an isolated point in time (e.g., blood pressure or core temperature). Perhaps a more robust and insightful diagnosis can be obtained by studying the functional interdependence of such indicators and the homeostasis that controls them. This requires quasi-continuous measurements and a procedure to map the data onto a parsimonious control model with a degree of universality.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7244502/The current research illustrates this approach using glucose homeostasis as a target. Data were obtained from 41 healthy subjects wearing over-the-counter glucose monitors, and projected onto a simple proportional–integral (PI) controller, widely used in engineering applications. The indicators quantifying the control function are clustered for the great majority of subjects, while a few outliers exhibit less responsive homeostasis. Practical implications for healthcare and education are further discussed.
Note that, in this case, your source was wrong, not just you. But, of course, you want to double down. Maybe you forgot that those weren't your words.Right.
It doesn't."Homeostasis of the body functions via mathematically balanced biological physics."
And what controls the chemical reactions? The action is physical, the function is mathematical.The body doesn't do maths. Homeostasis is about chemical reactions and neurology, not maths.
....Mathematics is the science and study of quality, structure, space, and change. Mathematicians seek out patterns, formulate new conjectures, and establish truth by rigorous deduction from appropriately chosen axioms and definitions.
Today, mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences.
Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new disciplines.
Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind, although practical applications for what began as pure mathematics are often discovered later.
:max_bytes(150000):strip_icc():format(webp)/examples-of-matter-608348-FINAL-5c891bba46e0fb0001431a70.jpg)
Abstract
Adaptation is an accommodation of system to external conditions. Adaptation is a widespread natural phenomenon. Simple one‐parametric adaptation occurs in the physics (for example, action is equal to counteraction). Adaptation has the wide circulation in economics (for example, balance of a supply and demand).
Most brightly multiple parameter adaptation is appeared in biology and physiology. However till now there was no trying of creation of the generalized mathematical apparatus of adaptation.
For the first time the mathematical description of two‐parametric adaptation (force and speed) has been applied to a discovery
«Effect of Force Adaptation in Mechanics».
The mathematical model of the adaptive mechanism which independently changes speed of motion under the action of external loading has been created. The adaptation mathematical apparatus has been used in hydraulics and in the electrical engineering.
Obviously there is a generalized mathematical regularity of adaptation.
https://www.researchgate.net/publication/303013778_Mathematical_Model_of_Adaptation
Sorry, that is not mathematics either. An accounting degree and book keeping and a degree in mathematics are very different animals.Then tell me what it is before I forget 7 years of integrated accounting of 7 separate community improvement programs, recording all facets of spending on needed supplies and labor, accounting for all allotted capital
I look at this from a more universal perspective.Sorry, that is not mathematics either. An accounting degree and book keeping and a degree in mathematics are very different animals.
Double-entry bookkeeping, also known as double-entry accounting, is a method of bookkeeping that relies on a two-sided accounting entry to maintain financial information. Every entry to an account requires a corresponding and opposite entry to a different account. The double-entry system has two equal and corresponding sides, known as debit and credit; this is based on the fundamental accounting principle that for every debit, there must be an equal and opposite credit.
A transaction in double-entry bookkeeping always affects at least two accounts, always includes at least one debit and one credit, and always has total debits and total credits that are equal. The purpose of double-entry bookkeeping is to allow the detection of financial errors and fraud.
https://en.wikipedia.org/wiki/Double-entry_bookkeepingDouble-entry bookkeeping is based on "balancing" the books, that is to say, satisfying the accounting equation. The accounting equation serves as an error detection tool; if at any point the sum of debits for all accounts does not equal the corresponding sum of credits for all accounts, an error has occurred. (However, satisfying the equation does not necessarily guarantee a lack of errors, for example, the wrong accounts could have been debited or credited.)
Do you want to know about STEM or not?I look at this from a more universal perspective.
Of course it is mathematics. It is a specialized area of mathematics and has been used for 500 years in balancing financial records.
Very much based on the model of; "For every action there is an equal and opposite reaction"( Newton's 3rd law)
Moreover, double entry accounting uses the same principles as maintaining homeostasis in living things.
Double-entry bookkeeping
https://en.wikipedia.org/wiki/Double-entry_bookkeeping
In business, this system is used to maintain the health of the organization.
In biology, this system is used to maintain the health of the living organism.
IMO, the lack of inclusion of bookkeeping as a mathematical discipline is not a fault of mathematics but of mathematicians...
No it isn't, it is checks and balances and arithmetic.I look at this from a more universal perspective.
Of course it is mathematics
No it isnt. Stop repeating the same stupid nonsense.In biology, this system is used to maintain the health of the living organism
Do you want to know about STEM or not?
Responding to QUANTITY differences of chemistry! Organs are physical objects, but their regulatory function is mathematical in essence.Homeostasis is ZERO to do with mathematics. It is organs, tissues, cells, hormones and neurotransmitters responding to CHEMISTRY
For the bacteria to use quorum sensing constitutively, they must possess three abilities: secretion of a signaling molecule, secretion of an autoinducer (to detect the change in concentration of signaling molecules), and regulation of gene transcription as a response.[10]
This process is highly dependent on the diffusion mechanism of the signaling molecules. QS signaling molecules are usually secreted at a low level by individual bacteria. At low cell density, the molecules may just diffuse away. At high cell density, the local concentration of signaling molecules may exceed its threshold level, and trigger changes in gene expression.[12]
Significant efforts have been made by teams of microbiologists and chemists to characterize the nature of the chemical signals involved in quorum sensing. This work has shown the importance of lactone homoserins in these exchanges. These are small organic molecules formed by a lactone nucleus and a carbon chain derived from fatty acids (Figure 2). They are very diversified: the length of the chain, the presence of double bonds or ketone groups, etc… allow to modulate the molecular “language”.
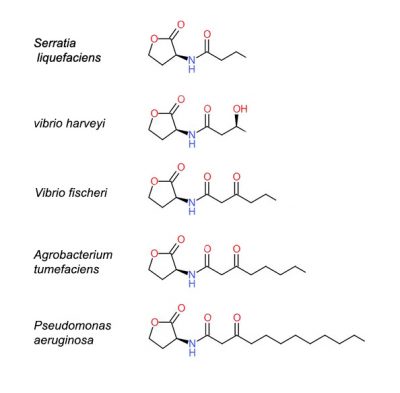
https://www.sciencedirect.com/science/article/abs/pii/S0166526X18300163#Quorum sensing is the response-regulation system of genes expression in accordance with the variation of cell population density. In this communication system, the response-regulation system induces group behaviors via signal molecules, which enabling cell acts actively to external environmental fluctuation.
What is Pattern Recognition?Pattern is everything around in this digital world. A pattern can either be seen physically or it can be observed mathematically by applying algorithms.
Example: The colors on the clothes, speech pattern, etc. In computer science, a pattern is represented using vector feature values.
https://www.geeksforgeeks.org/pattern-recognition-introduction/Pattern recognition is the process of recognizing patterns by using a machine learning algorithm. Pattern recognition can be defined as the classification of data based on knowledge already gained or on statistical information extracted from patterns and/or their representation. One of the important aspects of pattern recognition is its application potential.
Abstract
Vegetation science is concerned with a search for patterns, the discovery of processes giving rise to these patterns, and the uncovering of the mechanisms which ultimately cause such patterns and processes. The distinction between pattern, process and mechanism is rarely explicit in accounts of vegetation study, albeit always implied.
This can be traced to the difficulty of the task. I examine vegetation science in terms of its components, namely, pattern recognition, process definition and mechanism isolation, and identify the sources of difficulty. In doing so, I sketch the evolution of thought and methods in, reflecting upon the works of some major contributors. The critical phase is, of course, pattern recognition, which itself is at the mercy of the analytical tools, and, inherently, of perception. Once a pattern has been recognized, process and mechanism are inferred. The reliability of this is limited by the amount of observation that can be made on the system. The method of inference is also critical. In addition, scale effects complicate the picture.[/quote] Consequently, the connections between pattern, process and mechanism may be blurred. I emphasize the importance of scale and review some approaches to its study. [/quote]I stress the need for a clear distinction of these three concepts as a pre-requisite for clarity in studying vegetation. Most studies of vegetation dynamics deal with either describing pattern, or modelling process, but many fail to connect the two. It is even more rare to see patterns and processes predicted from underlying mechanisms. When such is attempted, it usually includes ambitious assumptions and far-fetched syntheses.
Although establishing the relationships between pattern, process and mechanism through inference thus entails several practical difficulties, it may be that the fundamental challenge lies in the theoretical complications.
Stability and uniqueness are properties characteristic of simple systems and induce facility in the establishment of cause-effect relationships.
https://www.jstor.org/stable/43461130Vegetation, however, is a complex system owing mainly to instability (small inputs leading to large and/or divergent outcomes), and plurality of causes and effects in its dynamics. It is likely that, as a consequence, the relationships between causes and effects (pattern, process and mechanism) are also complex. In essence, the problems identified may be ill-posed, rendering them more difficult to solve than previously thought. I illustrate these points and show that the search for understanding of these relationships predominates scientific inquiry.
MAnd what part of STEM do you think I need in order to understand principles of mathematics.
OK, pose a narrative question that is related to fundamental Mathematics.
