Janus58
Valued Senior Member
Just further evidence that you don't have the vaguest idea about what you are talking about.
How did the Earth capture the Moon ?
- Thread starter river
- Start date
river lives in a "Alice in Wonderland" world, and is so delusional as to believe it as fact. Actually sad.
Janus58
Valued Senior Member
The better question is why you think the mass/size of the captured body does matter.
OK smarty.....
OK river, I'm personally unable to use the mathematics of gravity and orbital parameters to prove to you what is already observed.
But in essence I don't have to. You are making the absurd claim that our Moon [and others like Charon] are impossible. Please now show us the maths that validate your position.
For the rest of the forum, obviously this wont happen...two reasons, river is unable to do it, and secondly, the maths tells us it is valid.
Another cop out!
Bye river...One thing I do need to learn, and that is to stop indulging fools, and trolls like yourself.
Thanks for reporting me by the way, it actually throws the spotlight [again] on what I have accused you of [lying and trolling] and what you previously have been banned from the sciences for. Perhaps the actions taken may be to your detriment.
Janus58
Valued Senior Member
Yes, they have, and they prove you to be wrong.
But in essence I don't have to. You are making the absurd claim that our Moon [and others like Charon] are impossible.
No I'm not .
I'm saying that Gravity simply is not the answer .
Last edited:
Your are actually bordering on psychotic delusional syndrome in actual fact.
Say what you like.For a person that did not know that just about everything in the universe rotates or has angular momentum, including the Moon, and that the Moon does not have a dark side, what you say is worth about zero.
https://www.physicsclassroom.com/class/circles/Lesson-4/Mathematics-of-Satellite-Motion
Mathematics of Satellite Motion
The motion of objects is governed by Newton's laws. The same simple laws that govern the motion of objects on earth also extend to the heavens to govern the motion of planets, moons, and other satellites. The mathematics that describes a satellite's motion is the same mathematics presented for circular motion in Lesson 1. In this part of Lesson 4, we will be concerned with the variety of mathematical equations that describe the motion of satellites.
[paste:font size="4"]net centripetal force acting upon this orbiting satellite is given by the relationship
Fnet = ( Msat • v2 ) / R
This net centripetal force is the result of the gravitational force that attracts the satellite towards the central body and can be represented as
Fgrav = ( G • Msat • MCentral ) / R2
Since Fgrav = Fnet, the above expressions for centripetal force and gravitational force can be set equal to each other. Thus,
(Msat • v2) / R = (G • Msat • MCentral ) / R2
Observe that the mass of the satellite is present on both sides of the equation; thus it can be canceled by dividing through by Msat. Then both sides of the equation can be multiplied by R, leaving the following equation.
v2 = (G • MCentral ) / R
Taking the square root of each side, leaves the following equation for the velocity of a satellite moving about a central body in circular motion
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the radius of orbit for the satellite.
[paste:font size="4"]Lesson 3, the equation for the acceleration of gravity was given as
g = (G • Mcentral)/R2
Thus, the acceleration of a satellite in circular motion about some central body is given by the following equation
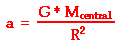
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the average radius of orbit for the satellite.
[paste:font size="4"]elsewhere, only the equation will be presented here. The period of a satellite (T) and the mean distance from the central body (R) are related by the following equation:
where T is the period of the satellite, R is the average radius of orbit for the satellite (distance from center of central planet), and G is 6.673 x 10-11 N•m2/kg2.
above. We will begin by determining the orbital speed of the satellite using the following equation:
v = SQRT [ (G•MCentral ) / R ]
The substitution and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg)/ (6.47 x 106 m) ]
v = 7.85 x 103 m/s
The acceleration can be found from either one of the following equations:
(1) a = (G • Mcentral)/R2(2) a = v2/R
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the acceleration. The use of equation (1) will be demonstrated here.
a = (G •Mcentral)/R2
a = (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg) / (6.47 x 106 m)2
a = 9.53 m/s2
Observe that this acceleration is slightly less than the 9.8 m/s2 value expected on earth's surface. As discussed in Lesson 3, the increased distance from the center of the earth lowers the value of g.
Finally, the period can be calculated using the following equation:
The equation can be rearranged to the following form
T = SQRT [(4 • pi2 • R3) / (G*Mcentral)]
The substitution and solution are as follows:
T = SQRT [(4 • (3.1415)2 • (6.47 x 106 m)3) / (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ]
T = 5176 s = 1.44 hrs
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the orbital speed; the use of equation (1) will be demonstrated here. The substitution of values into this equation and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2)*(5.98x1024 kg)/ (3.82 x 108 m) ]
v = 1.02 x 103 m/s
http://www.satsig.net/sslist.htm. Use the Satellite Information widget below to explore the various properties - speed, height, orbital path, etc. - of any existing satellite. Simply type in the name (correctly) of the satellite and click on the Get Information button
Mathematics of Satellite Motion
- Kepler's Three Laws
- Circular Motion Principles for Satellites
- Mathematics of Satellite Motion
- Weightlessness in Orbit
- Energy Relationships for Satellites
The motion of objects is governed by Newton's laws. The same simple laws that govern the motion of objects on earth also extend to the heavens to govern the motion of planets, moons, and other satellites. The mathematics that describes a satellite's motion is the same mathematics presented for circular motion in Lesson 1. In this part of Lesson 4, we will be concerned with the variety of mathematical equations that describe the motion of satellites.
[paste:font size="4"]net centripetal force acting upon this orbiting satellite is given by the relationship
Fnet = ( Msat • v2 ) / R
This net centripetal force is the result of the gravitational force that attracts the satellite towards the central body and can be represented as
Fgrav = ( G • Msat • MCentral ) / R2
Since Fgrav = Fnet, the above expressions for centripetal force and gravitational force can be set equal to each other. Thus,
(Msat • v2) / R = (G • Msat • MCentral ) / R2
Observe that the mass of the satellite is present on both sides of the equation; thus it can be canceled by dividing through by Msat. Then both sides of the equation can be multiplied by R, leaving the following equation.
v2 = (G • MCentral ) / R
Taking the square root of each side, leaves the following equation for the velocity of a satellite moving about a central body in circular motion
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the radius of orbit for the satellite.
[paste:font size="4"]Lesson 3, the equation for the acceleration of gravity was given as
g = (G • Mcentral)/R2
Thus, the acceleration of a satellite in circular motion about some central body is given by the following equation
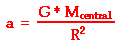
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the average radius of orbit for the satellite.
[paste:font size="4"]elsewhere, only the equation will be presented here. The period of a satellite (T) and the mean distance from the central body (R) are related by the following equation:
where T is the period of the satellite, R is the average radius of orbit for the satellite (distance from center of central planet), and G is 6.673 x 10-11 N•m2/kg2.
above. We will begin by determining the orbital speed of the satellite using the following equation:
v = SQRT [ (G•MCentral ) / R ]
The substitution and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg)/ (6.47 x 106 m) ]
v = 7.85 x 103 m/s
The acceleration can be found from either one of the following equations:
(1) a = (G • Mcentral)/R2(2) a = v2/R
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the acceleration. The use of equation (1) will be demonstrated here.
a = (G •Mcentral)/R2
a = (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg) / (6.47 x 106 m)2
a = 9.53 m/s2
Observe that this acceleration is slightly less than the 9.8 m/s2 value expected on earth's surface. As discussed in Lesson 3, the increased distance from the center of the earth lowers the value of g.
Finally, the period can be calculated using the following equation:
The equation can be rearranged to the following form
T = SQRT [(4 • pi2 • R3) / (G*Mcentral)]
The substitution and solution are as follows:
T = SQRT [(4 • (3.1415)2 • (6.47 x 106 m)3) / (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ]
T = 5176 s = 1.44 hrs
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the orbital speed; the use of equation (1) will be demonstrated here. The substitution of values into this equation and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2)*(5.98x1024 kg)/ (3.82 x 108 m) ]
v = 1.02 x 103 m/s
http://www.satsig.net/sslist.htm. Use the Satellite Information widget below to explore the various properties - speed, height, orbital path, etc. - of any existing satellite. Simply type in the name (correctly) of the satellite and click on the Get Information button
https://www.physicsclassroom.com/class/circles/Lesson-4/Mathematics-of-Satellite-Motion
Mathematics of Satellite Motion
- Kepler's Three Laws
- Circular Motion Principles for Satellites
- Mathematics of Satellite Motion
- Weightlessness in Orbit
- Energy Relationships for Satellites
The motion of objects is governed by Newton's laws. The same simple laws that govern the motion of objects on earth also extend to the heavens to govern the motion of planets, moons, and other satellites. The mathematics that describes a satellite's motion is the same mathematics presented for circular motion in Lesson 1. In this part of Lesson 4, we will be concerned with the variety of mathematical equations that describe the motion of satellites.
[paste:font size="4"]net centripetal force acting upon this orbiting satellite is given by the relationship
Fnet = ( Msat • v2 ) / R
This net centripetal force is the result of the gravitational force that attracts the satellite towards the central body and can be represented as
Fgrav = ( G • Msat • MCentral ) / R2
Since Fgrav = Fnet, the above expressions for centripetal force and gravitational force can be set equal to each other. Thus,
(Msat • v2) / R = (G • Msat • MCentral ) / R2
Observe that the mass of the satellite is present on both sides of the equation; thus it can be canceled by dividing through by Msat. Then both sides of the equation can be multiplied by R, leaving the following equation.
v2 = (G • MCentral ) / R
Taking the square root of each side, leaves the following equation for the velocity of a satellite moving about a central body in circular motion
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the radius of orbit for the satellite.
[paste:font size="4"]Lesson 3, the equation for the acceleration of gravity was given as
g = (G • Mcentral)/R2
Thus, the acceleration of a satellite in circular motion about some central body is given by the following equation
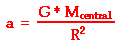
where G is 6.673 x 10-11 N•m2/kg2, Mcentral is the mass of the central body about which the satellite orbits, and R is the average radius of orbit for the satellite.
[paste:font size="4"]elsewhere, only the equation will be presented here. The period of a satellite (T) and the mean distance from the central body (R) are related by the following equation:
where T is the period of the satellite, R is the average radius of orbit for the satellite (distance from center of central planet), and G is 6.673 x 10-11 N•m2/kg2.
above. We will begin by determining the orbital speed of the satellite using the following equation:
v = SQRT [ (G•MCentral ) / R ]
The substitution and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg)/ (6.47 x 106 m) ]
v = 7.85 x 103 m/s
The acceleration can be found from either one of the following equations:
(1) a = (G • Mcentral)/R2(2) a = v2/R
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the acceleration. The use of equation (1) will be demonstrated here.
a = (G •Mcentral)/R2
a = (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg) / (6.47 x 106 m)2
a = 9.53 m/s2
Observe that this acceleration is slightly less than the 9.8 m/s2 value expected on earth's surface. As discussed in Lesson 3, the increased distance from the center of the earth lowers the value of g.
Finally, the period can be calculated using the following equation:
The equation can be rearranged to the following form
T = SQRT [(4 • pi2 • R3) / (G*Mcentral)]
The substitution and solution are as follows:
T = SQRT [(4 • (3.1415)2 • (6.47 x 106 m)3) / (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ]
T = 5176 s = 1.44 hrs
above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the orbital speed; the use of equation (1) will be demonstrated here. The substitution of values into this equation and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2)*(5.98x1024 kg)/ (3.82 x 108 m) ]
v = 1.02 x 103 m/s
http://www.satsig.net/sslist.htm. Use the Satellite Information widget below to explore the various properties - speed, height, orbital path, etc. - of any existing satellite. Simply type in the name (correctly) of the satellite and click on the Get Information button
And therefore what pad ?
Gravity is the dominant force and is what shapes the universe, forms planets and moons, facilitates orbits etc etc
Read up on some science and stop being a troll.
No just clearing up your nonsense.
And it is also infinite in its extent as well as acting on everything and the force which shapes the universe.