Motor Daddy
Valued Senior Member
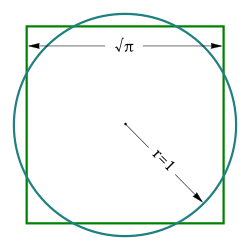
A square of 3.14 units of square area that is equal to the circle area has sides of length $$sqrt{3.14}=1.772004514666935$$ units.
rpenner, You state the ratio of lengths AB:CD = 1:√3 in my diagram.
I stated the above, which means the lengths of the sides are 1.772004514666935 units, not as you state "1:√3" which is 1.732050807568877 units.
Care to take another stab at it?