Does Chaos Theory prove a Mathematically Ordered Universe

[Write4U]

Good point .
Where then do mathematics come from then ?

That is the pertinent question.
IMO, everything that can be measured and translated into a symbolic representation is of "logical necessity" a mathematical construct.
It is what allows us to posit universal constants, the laws that govern the dynamical evolution of universally pervasive patterns such as; fractals, functions, equations, exponential functions, symmetry/symmetry breaking, invariants; [/quote]
Invariant (mathematics)

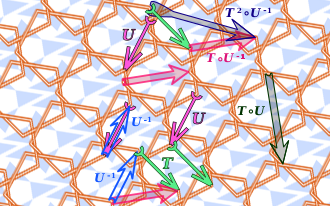
A wallpaper is invariant under an infinite number of translations, members of a group, of which the operation denoted by (o) is the function composition.

In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects.[1][2][3] The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used.[1] More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class.[4]

Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an important step in the process of classifying mathematical objects.[3][4]

https://en.wikipedia.org/wiki/Invariant_(mathematics)

Symmetry in mathematics


The root system of the exceptional Lie group E8. Lie groups have many symmetries.

Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.[1][2]

Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This can occur in many ways; for example, if X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (i.e., an isometry).

In general, every kind of structure in mathematics will have its own kind of symmetry, many of which are listed in the given points mentioned above.

https://en.wikipedia.org/wiki/Symmetry_in_mathematics

The exponential function
Overview of the exponential function

The exponential function is one of the most important functions in mathematics (though it would have to admit that the linear function ranks even higher in importance).

To form an exponential function, we let the independent variable be the exponent. A simple example is the function: f(x) = 2x.
In mathematics, a function[note 1] is a binary relation between two sets that associates to each element of the first set exactly one element of the second set. Typical examples are functions from integers to integers, or from the real numbers to real numbers

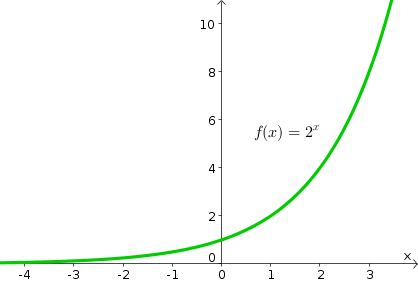
As illustrated in the above graph of (f) the exponential function increases rapidly. Exponential functions are solutions to the simplest types of dynamical systems. For example, an exponential function arises in simple models of bacteria growth.

An exponential function can describe growth or decay. The function: g(x)=(12)x

https://mathinsight.org/exponential_function

continued....

 

[Write4U]

continued....

Equation
What is an equation?

In algebra, an equation can be defined as a mathematical statement consisting of an equal symbol between two algebraic expressions that have the same value.

The most basic and common algebraic equations in math consist of one or more variables.
For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an ‘equal’ sign.

https://www.splashlearn.com/math-vocabulary/number-sense/equation#

Function

Schematic depiction of a function described metaphorically as a "machine" or "black box" that for each input yields a corresponding output

In mathematics, a function is a binary relation between two sets that associates to each element of the first set exactly one element of the second set. Typical examples are functions from integers to integers, or from the real numbers to real numbers

https://en.wikipedia.org/wiki/Function_(mathematics)

Fractal

In mathematics, a fractal is a subset of Euclidean space with a fractal dimension that strictly exceeds its topological dimension. Fractals appear the same at different scales, as illustrated in successive magnifications of the Mandelbrot set.[1][2][3][4]

Fractals exhibit similar patterns at increasingly smaller scales, a property called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge,[5] it is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

https://en.wikipedia.org/wiki/Fractal

And self-similarity also refers to self-referential and ultimately to self-awareness.

These are some of the universal constants which are not based on any physical consideration but on the abstract logic of how things work and are pervasive throughout the universe

 

[exchemist]

ZZZzzzz..........

 

[river]

river said: ↑
Good point .


Where then do mathematics come from then ?

The Physical depth of shape . Fundamentally , Three dimensions . Depth , Breadth , and length .

 

[Beaconator]

Prove its non-sense . Care to Discuss with me ?

Pure energy could not be confined within a galaxy. Absolute zero is only available outside the universe and no where near black holes supermassive or not. So ...

 

[Beaconator]

The Physical depth of shape . Fundamentally , Three dimensions . Depth , Breadth , and length .

You forgot time, which includes “entropy”

 

[Write4U]

Chaos Theory and Consciousness
POSTED AUGUST 1, 2020 ARPAN DEY

Abstract

Consciousness remains one of the most bizarre phenomena in the universe. Though a well-researched field, science is still to reveal the fundamental nature of consciousness. This is perhaps due to the fact that consciousness is not entirely a biological phenomenon but rather an emergent process, rising out of complex interactions between simpler parts, in a large system.

On the other hand, chaos theory[1] is the branch of mathematics dealing with complex, dynamical systems. Chaos theory has wide-ranging applications – from weather prediction and market research to crowd management and heartbeat inequalities. Fractals[2] form an integral part of chaos theory, and prove that it is possible to generate complex, real-life patterns mathematically.

The question addressed in this article is whether chaos theory can reproduce the complex interactions that give rise to consciousness itself. Consciousness must be treated differently, at a fundamental stage. Once the fundamental nature of consciousness is clear, it is easier to predict its behavior. While it is beyond the scope of present science to achieve this feat, it is reasonable enough to assume that mathematics can, in principle, reproduce the complex patterns and interactions that give rise to consciousness.

.......more

https://ysjournal.com/chaos-theory-and-consciousness/#

 

[river]

Chaos Theory and Consciousness
POSTED AUGUST 1, 2020 ARPAN DEY

Abstract .......more

https://ysjournal.com/chaos-theory-and-consciousness/#

 

[river]

Consciousness is Based on Life .

 

[Write4U]

Consciousness is Based on Life .

That's debatable.

From the link:

On the other hand, chaos theory[1] is the branch of mathematics dealing with complex, dynamical systems. Chaos theory has wide-ranging applications – from weather prediction and market research to crowd management and heartbeat inequalities. Fractals[2] form an integral part of chaos theory, and prove that it is possible to generate complex, real-life patterns mathematically.

https://ysjournal.com/chaos-theory-and-consciousness/#

Seems to me that this is what Tegmark proposes. Consciousness is not exclusively biological, but may also emerge from mathematical data processing patterns, i.e. AI consciousness.

 

[river]

That's debatable.

From the link: https://ysjournal.com/chaos-theory-and-consciousness/#

Seems to me that this is what Tegmark proposes. Consciousness is not exclusively biological, but may also emerge from mathematical data processing patterns, i.e. AI consciousness.

but not Real Life . As in Biological Life .

 

[Write4U]

but not Real Life . As in Biological Life .

Show me the difference. It's all made from the same stuff, just arranged in different patterns.
It's the patterns that acquire emergent properties. I have heard that only biological patterns can be alive, but I have never heard that only biological patterns can be conscious. Are you sure? Can you explain?

 

[river]

river said: ↑
but not Real Life . As in Biological Life .

Show me the difference. It's all made from the same stuff, just arranged in different patterns.
It's the patterns that acquire emergent properties. I have heard that only biological patterns can be alive, but I have never heard that only biological patterns can be conscious. Are you sure? Can you explain?

Life comes from Nature , from the Cosmos .

AI can not exist on its own . It needs a being to build it . Life does not .

 

[Write4U]

Life comes from Nature , from the Cosmos .

AI can not exist on its own . It needs a being to build it . Life does not .

Really?
Is a virus alive? It also cannot exist on its own, but it can use a living organism to build copies of itself. Variegated tulips are artificially made by viruses.

Variegated Tulips: Beauty From a Virus

Have you ever seen tulips like these, tulips that look like they've been 'painted' with multiple colors? ... However, in the 1600s when these variegated tulips first came into popularity, the “breaks” in coloring were, in fact, caused by a virus in the bulb called tulip break virus, which was carried by aphids.Mar 29, 2018

Viruses using aphids to do the heavy lifting!

Section 6.3Viruses: Structure, Function, and Uses

A virus is a small parasite that cannot reproduce by itself. Once it infects a susceptible cell, however, a virus can direct the cell machinery to produce more viruses.

Most viruses have either RNA or DNA as their genetic material. The nucleic acid may be single- or double-stranded. The entire infectious virus particle, called a virion, consists of the nucleic acid and an outer shell of protein. The simplest viruses contain only enough RNA or DNA to encode four proteins. The most complex can encode 100 – 200 proteins.

https://www.ncbi.nlm.nih.gov/books/NBK21523/#

 

[river]

Really?
Is a virus alive? It also cannot exist on its own, but it can use a living organism to build copies of itself. Variegated tulips are artificially made by viruses.

Variegated Tulips: Beauty From a Virus Viruses using aphids to do the heavy lifting!

Section 6.3Viruses: Structure, Function, and Uses https://www.ncbi.nlm.nih.gov/books/NBK21523/#

So viruses do not come from Nature ? They do of course . So what's your point Write4U ?

 

[exchemist]

Pure energy could not be confined within a galaxy. Absolute zero is only available outside the universe and no where near black holes supermassive or not. So ...

"Pure energy" is for Star Trekkies.

It is not science.

 

[Write4U]

So viruses do not come from Nature ? They do of course . So what's your point Write4U ?

Variegated tulips do not come from nature. They are artificially created by viruses, clever little artists manipulating the tulip genes to make some of the most beautiful art.
Robots are artificially created by humans, clever mammals making tools to do all their work for them.

 

[river]

Variegated tulips do not come from nature. They are artificially created by viruses, clever little artists manipulating the tulip genes to make some of the most beautiful art.
Robots are artificially created by humans, clever mammals making tools to do all their work for them.

Viruses do .

Tools agreed . Lets hope that these tools are nothing more than tools .

 

[Write4U]

Viruses do .

Tools agreed . Lets hope that these tools are nothing more than tools .

What is the distinction? Energy is "ability to do work" regardless of instrument used.
A star has ability to do use nuclear reactions (work) to create energy and other works of Art.

Stars produce energy from nuclear reactions, primarily the fusion of hydrogen to form helium. These and other processes in stars have lead to the formation of all the other elements.

Natura Artis Magistra (nature is the teacher of art and science)

Natura artis magistra
Linguistics in the Netherlands 2001, 159–166. issn 0929–7332 © 2001 John Benjamins Publishing Company Ancient rhetoricians, grammarians and philosophers on natural word order* C.C. de Jonge Leiden University

1. Introduction

The idea that nature is to be taken as an example in life in general and in the artes in particular occurs frequently in antiquity. According to Democritus, human beings are “the pupils of the animals”. The Stoic philosophers felt that man must live in accordance with nature and also Epicurus held up nature as an example for humanity.

1. The idea of nature is one of the most complex concepts we can talk about in language and this applies to the Greek word phusis and the Latin word natura as well. When we speak of nature or natural we can mean various things:

2. to begin with nature may be used to refer to the character or essence of a thing. In that case what is unnatural is unusual. Sometimes nature coincides with the whole of the perceptible world.

3. We can also find the idea that nature is to be taken as a model in ancient views of language: ancient rhetoricians, grammarians and philosophers all mention a 160 C.C. de Jonge theory of the existence of a natural word order. The wide dissemination of the concept of natural word order rather obscures the important differences which lurk behind the single term.

4. It appears that the idea of a natural word order was used on three levels: practical, theoretical and philosophical. The rhetoricians derived principles for word order in the strict sense from nature. The grammarian Apollonius Dyscolus defended a theory of the hierarchy of the parts of speech, which appears to have more consequences for the grammatical discussion of these parts of speech than for practical sentence construction. Finally, the Stoic philosophers assumed that there was a certain hierarchy among the categories to which words refer.

https://www.jbe-platform.com/docserver/fulltext/avt.18.17jon.pdf

 

[river]

What is the distinction? Energy is "ability to do work" regardless of instrument used.
A star has ability to do use nuclear reactions (work) to create energy and other works of Art.
Natura Artis Magistra (nature is the teacher of art and science)

Natura artis magistra
Linguistics in the Netherlands 2001, 159–166. issn 0929–7332 © 2001 John Benjamins Publishing Company Ancient rhetoricians, grammarians and philosophers on natural word order* C.C. de Jonge Leiden University

1. Introduction
https://www.jbe-platform.com/docserver/fulltext/avt.18.17jon.pdf

Your point Write4U .