Fundamental confusions of calculus

[RJBeery]

There's a greater irony in there.

If that's a dig at me I'm missing it... :bawl:

 

[przyk]

I simply constructed a function for Pete to calculate the total derivative.

Then that's

$$
\frac{\mathrm{d}T}{\mathrm{d}t} \,=\, \frac{\partial T}{\partial t} \,+\, \frac{\partial T}{\partial x} \, \frac{\mathrm{d}x}{\mathrm{d}t} \,+\, \frac{\partial T}{\partial y} \, \frac{\mathrm{d}y}{\mathrm{d}t} \,+\, \frac{\partial T}{\partial z} \, \frac{\mathrm{d}z}{\mathrm{d}t} \,.
$$​

This requires $$z$$ to be cast as a function of $$t$$, even if you make it a constant function. If it's a constant function, then $$\frac{\mathrm{d}z}{\mathrm{d}t} = 0$$, and only then can you say that

$$
\frac{\mathrm{d}T}{\mathrm{d}t} \,=\, \frac{\partial T}{\partial t} \,+\, \frac{\partial T}{\partial x} \, \frac{\mathrm{d}x}{\mathrm{d}t} \,+\, \frac{\partial T}{\partial y} \, \frac{\mathrm{d}y}{\mathrm{d}t} \,.
$$​

Do you have any problem with this?

If you don't make $$z$$ a constant function of $$t$$, and simply leave it as an independent parameter, then you're still taking a partial derivative. Do you understand the difference?

 

[Trippy]

If that's a dig at me I'm missing it... :bawl:

No, it's a reference to Tach's (apparent) habit of not reading posts completely, and jumping in at the deep-end at the first thing he comes accross that he doesn't like. It's also a reference to his apparent inability to spot an equivalent solution.

For example, consider Tach's objection:

Sure, IF you were given the above. But what you are being given is

$$f(\theta, u(\theta),v)=3\theta+u+v$$ where $$u(\theta)=sin^2(\theta)$$, $$v(x)=ln(x)$$

The total derivative will be the same but the partial derivative differs , depending on what you consider that has been given as $$f$$.

Now, compare it to this:

Then I would set:
$$u=sin(\theta)$$
Then I would find:
$$\frac{df}{du}$$ for the equation $$f(\theta)=3 \theta+u^2+k$$
And find:
$$\frac{du}{d \theta}$$ for $$u=sin(\theta)$$
And then proceed to evaluate: $$\frac{\partial f}{\partial \theta} = \frac{df}{du}\frac{du}{d \theta}$$

And this:

But that, to me, seems unneccessary, when the initial problem is relatively uncomplicated.

It seemd to me that what you've done is redefined the problem as being:
$$f(\theta,x)=g(\theta)+h(\theta)+i(x)$$
And then come to the conclusion that $$f'(\theta)=g'(\theta)$$ while neglecting to evaluate $$h'(\theta)$$

Even considering this:

$$f(\theta, u(\theta),v)=3\theta+u+v$$ where $$u(\theta)=sin^2(\theta)$$, $$v(x)=ln(x)$$

I would expect that the first thing most people would do would be to substitute $$u(\theta)=sin^2(\theta)$$ back into $$f(\theta, u(\theta),v)=3\theta+u+v$$

And then proceed to work with $$f(\theta,v)=3\theta+sin^2(\theta)+v$$ to find $$\frac{\partial f}{\partial \theta}$$.

 

[RJBeery]

Ahh yes. I'm sincerely curious to know the degree to which peoples' subconscious minds blind them from inconvenient posts. This is something that I study quite a bit in politics, for example, but confirmation bias is more difficult to pull off in pure science (particularly math!).

 

[AlphaNumeric]

You got it totally backwards, let's try it one more time: partial derivative means that if $$f=f(t,u)$$ where $$u=u(t)$$ then $$\frac{\partial f}{\partial t}$$ is the partial derivative while $$\frac{\partial f}{\partial t}+\frac{\partial f}{\partial u}\frac{du}{dt}$$ is the total derivative.Partial derivative means differentiation only wrt the explicit variable (t in the example), total derivative means partial derivative PLUS differentiation (via chain rule) through all variables that are a function of the variable considered. Therefore, contrary to your claims, I know exactly what I am doing and the method described (it is textbook, really) produces the correct answer:

So, $$p=\frac{\partial T}{\partial \dot{q}}=m\dot{q}$$

No contradiction of any sort.

Except that $$\dot{q}^{2}$$ is a function of the variable in question. Why didn't you change that to say $$v(\dot{q})$$? Why is $$\partial_{\theta}(\sin^{2}\theta) = 0$$ but $$\partial_{\dot{q}}(\dot{q}^{2}) \neq 0$$? You're being inconsistent. Furthermore what about the pendulum potential, which involves a $$\cos \theta$$ term? If $$L = \frac{1}{2}ml^{2}\dot{\theta}^{2} + mgl \cos \theta$$ and the Euler-Lagrange equation is $$\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta}} \right) = \frac{\partial L}{\partial \theta}$$ then by your logic the equation of motion is $$ml^{2}\ddot{\theta} = 0$$, which it obviously isn't.

You didn't address that when I brought it up. Repeatedly. Hence why I question whether you actually know any Lagrangian/Hamiltonian mechanics because the most trivial examples immediately falsify your claim. If your claim was right the pendulum wouldn't behave as it does. The only total derivative in the E-L equation is the time derivative, all others are partial and the trig term doesn't vanish.

I can track your error to the fact that you failed repeatedly to note that in my example, $$f=3 \theta +u+v$$ and you kept considering that $$f=3 \theta +sin^2(\theta)+v$$. So, you are getting the wrong partial derivative. Not a big error, but please don't try to pin it on me, own it.

You're the one who said $$\partial_{\theta}(3 \theta +sin^2(\theta)+v) = 3$$. That's what I'm addressing. Yes, if you start with $$f(\theta,u,v)$$ then you need to do something slightly different because it's a different function. As has been pointed out to you repeatedly, you don't seem to realise you're altering the problem at hand.

You haven't managed to show a mistake in my use of the definition, you just keep saying "The book!" and considering something else.

No doubt you'll proclaim "Argument from authority!" but I mentioned this to my work colleagues today. 5 PhDs in maths and physics went "WTF? How can he be that mistaken!". That brings the count of doctorates disagreeing with you I've spoken to up to 10. Such a shame you're going down the same path as Reiku and mindlessly sticking to "Look, this source I think backs me up!". Each time you've done that you've had your misunderstanding explained to you. Unfortunately I don't think you have sufficient understanding/experience to grasp any subtle issues which arise and thus cannot get your head around this stuff.

 

[przyk]

Of course, in your trolling haste, you failed to notice that $$f(\theta,u,v)=3 \theta+u+v$$ where $$u=sin^2(\theta)$$ and $$v=ln(x)$$.

In your own trolling haste, you failed to notice that contradicts the material quoted. You yourself literally used $$f(\theta,\, x)$$ there:

If x and $$\theta$$ are independent variables...

$$f(\theta, x) =3 \theta+ sin^2(\theta)+ln(x) \\
\frac{\partial }{\partial \theta} f(\theta, x)= 3 + 2 \sin(\theta) \cos (\theta)$$​

Your claim that $$\frac{\partial }{\partial \theta} f(\theta, x)= 3 + 2 \sin(\theta) \cos (\theta)$$ is outright wrong because it shows that you do not understand the meaning of partial differentiation.

And as things are written here, Pete was correct and your response was utter bullshit. Maybe you've learned something since, but evidently at the time you had misconceptions about partial differentiation.

 

[Tach]

No, that's exactly what we were given:
Post #18


If you meant something else, perhaps you should be more careful in the future.

Here is the complete post:

The difference between total derivative and partial derivative is really simple, Pete, and it was spelled out quite clearly in the post you quoted: partial derivative is taken with respect to $$\theta$$ being an explicit argument, total derivative is the sum of the partial derivative (if it exists) plus the chain derivatives due to certain arguments being functions of $$\theta$$. You do not need to spread the same question over three threads in order to understand this.
In math terms: if $$f=f(\theta, u(\theta),v,w,...)$$

then:


The total derivative wrt $$\theta$$is:


$$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u} \frac{du}{d \theta}$$

while the partial derivative wrt $$\theta$$ is:

$$\frac{\partial f}{\partial \theta}$$

Example:

$$f=3 \theta+ sin^2(\theta)+ln(x)$$

$$\frac{df}{d \theta}=3+2 sin(\theta) cos (\theta)$$

$$\frac{\partial f}{\partial \theta}=3$$

It it takes extreme bad faith not to see that the post is about $$f=f(\theta, u(\theta),v,w,...)$$ and $$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u} \frac{du}{d \theta}$$.

The most amazing thing is that three moderators (AN, you and prometheus) and three people with advanced degrees (przyk, Guest254 and rpenner) have failed to see the above, despite being pointed out to them repeatedly.

 

[Tach]

Except that $$\dot{q}^{2}$$ is a function of the variable in question. Why didn't you change that to say $$v(\dot{q})$$?

Because this is NOT the way the function is presented. If someone was so perverse to define $$T=\frac{m u^2}{2}$$ with $$u(\dot {q})=\dot {q}$$ only THEN $$\frac{\partial T}{\partial \dot {q}}=0$$.

Why is $$\partial_{\theta}(\sin^{2}\theta) = 0$$

It isn't , but you really need to be willing to listen.

but $$\partial_{\dot{q}}(\dot{q}^{2}) \neq 0$$?

See above, it is really simple.

Yes, if you start with $$f(\theta,u,v)$$ then you need to do something slightly different because it's a different function.

...which is precisely at the top of post 18. It takes extreme bad faith not to recognize $$u(\theta)$$ as $$sin^2(\theta)$$ in the description of $$f(\theta, u(\theta), v)$$ ESPECIALLY in the context of the whole post being about the fact that $$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u}\frac{du}{d \theta}$$

 

[rpenner]

Everyone is crazy and wrong except you, Tach, eh?

 

[Tach]

I would expect that the first thing most people would do would be to substitute $$u(\theta)=sin^2(\theta)$$ back into $$f(\theta, u(\theta),v)=3\theta+u+v$$

Err, what you expect and what the books say are two different things. The books say that you don't do this substitution.

And then proceed to work with $$f(\theta,v)=3\theta+sin^2(\theta)+v$$ to find $$\frac{\partial f}{\partial \theta}$$.

...and that would be the perfectly ok thing to do IF you were asked to compute the total derivative.

....and, by the same token, this would be the wrong thing to do if you were asked to calculate the partial derivative wrt $$\theta$$

Look, the fact that so many people with advanced degrees in math miss this simple thing is nothing short of amazing. The fact that six of you (AN, you, rpenner, przyk, Guest254, prometheus) argue(d) against only one of me doesn't make you right and me wrong. At least, prometheus stopped arguing, once he realized that he might be on the wrong side of the argument.

 

[Tach]

Everyone is crazy and wrong except you, Tach, eh?

I didn't say that any of you is crazy. But I do think that you are arguing in bad faith. You know a lot of math, you should have figured out by now that you are on the wrong side of the argument. Especially, after you have been told repeatedly about the "chain rule" in $$f=f(\theta, u(\theta),v(x))$$. If you were arguing in good faith, seeing $$f=f(\theta, u(\theta),v(x))$$ would have sufficed to make you stop.

 

[arfa brane]

So, to recap, what Penrose is talking about and what the "fundamental confusions" are and how to avoid them is:

1) Don't confuse the function with its value at some point.
2) Don't confuse the index notation (which variables are constant) when going from patch to patch.


So if we have a function of two variables like this:

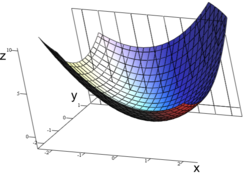
A graph of z = x[sup]2[/sup] + xy + y[sup]2[/sup].

Then the contour lines on the graph are just the lines of constant x or y. So we make new functions of one variable: $$ \partial_x $$ and/or $$ \partial_y $$ where x and y are constant in each case, and are now treated as indices.

So each new function defines a 'slice' through the total function, which is plane-parallel to either yz or xz:

A slice of the graph above at y= 1


So the family of functions is the family of slices plane-parallel to either yz or xz. So the functions are really like $$ \partial_{x_i} $$ for i slices.

 

[temur]

The difference between total derivative and partial derivative is really simple, Pete, and it was spelled out quite clearly in the post you quoted: partial derivative is taken with respect to $$\theta$$ being an explicit argument, total derivative is the sum of the partial derivative (if it exists) plus the chain derivatives due to certain arguments being functions of $$\theta$$. You do not need to spread the same question over three threads in order to understand this.
In math terms: if $$f=f(\theta, u(\theta),v,w,...)$$

then:


The total derivative wrt $$\theta$$is:


$$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u} \frac{du}{d \theta}$$

while the partial derivative wrt $$\theta$$ is:

$$\frac{\partial f}{\partial \theta}$$

Example:

$$f=3 \theta+ sin^2(\theta)+ln(x)$$

$$\frac{df}{d \theta}=3+2 sin(\theta) cos (\theta)$$

$$\frac{\partial f}{\partial \theta}=3$$

If this is what you guys are arguing about, Tach is wrong. He is wrong about the total derivative, and at best did not communicate his knowledge about partial derivative well. If somebody wrote this on an exam paper he would get no mark.

 

[Trippy]

It it takes extreme bad faith not to see that the post is about $$f=f(\theta, u(\theta),v,w,...)$$ and $$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u} \frac{du}{d \theta}$$.

You want to talk about bad faith?

First you say:

In math terms: if $$f=f(\theta, u(\theta),v,w,...)$$

then:

The total derivative wrt $$\theta$$is:

$$\frac{df}{d \theta}=\frac{\partial f}{\partial \theta}+\frac{\partial f}{\partial u} \frac{du}{d \theta}$$

while the partial derivative wrt $$\theta$$ is:

$$\frac{\partial f}{\partial \theta}$$

Example:

$$f=3 \theta+ sin^2(\theta)+ln(x)$$

$$\frac{df}{d \theta}=3+2 sin(\theta) cos (\theta)$$

$$\frac{\partial f}{\partial \theta}=3$$

Which tells us nothing, other than what I quoted, because you neither define nor use u in this.

Then you agree to Prom's interpretation

I want to be very clear about this: You're saying that $$\frac{\partial }{\partial \theta}\left(3 \theta+ sin^2(\theta)+ln(x) \right)=3$$?

Yes, do you have a problem with this?

Which likewise doesn't use u, and leaves it undefined.

It's not until nearly ten posts after you post the example that you get around to defining u, and in so doing redefining f:

Er, nope. As written, $$\frac{\partial}{\partial \theta} \Bigl( 3 \theta \,+\, \sin(\theta)^{2} \,+\, \ln(x) \Bigr) \,=\, 3 \,+\, \sin(2\theta)$$.

Err, wrong. Partial derivative means derivative wrt the explicit variable only. What you took is the total derivative wrt $$\theta$$. Think about:

$$f(\theta,u,x)=3 \theta +u^2+ln(x)$$

where $$u=sin(\theta)$$.

And then by post 80-something, you've changed your definition of u, and introduced v, and redfined f.

Yes, you did work through but you worked incorrectly. In the book I cited, there are a lot of exercises, they all contradict your claims. Look, it is very simple:

$$f=f(\theta, u,v)$$

$$u=sin^2(\theta)$$
$$v=ln(x)$$
$$f=3 \theta+u+v$$[/tex]

The most amazing thing is that three moderators (AN, you and prometheus) and three people with advanced degrees (przyk, Guest254 and rpenner) have failed to see the above, despite being pointed out to them repeatedly.

You're not really in a position to invest this much emotional currency in being right.

As I said, perhaps in future you could be more careful.

 

[Trippy]

Look, the fact that so many people with advanced degrees in math miss this simple thing is nothing short of amazing. The fact that six of you (AN, you, rpenner, przyk, Guest254, prometheus) argue(d) against only one of me doesn't make you right and me wrong.

The only confusion stems from your inability to articulate your thoughts accurately.

 

[rpenner]

At least, prometheus and rpenner stopped arguing, once he realized that they he might be on the wrong side of the argument.

You have no basis on which to assert that prometheus and I have stopped arguing and certainly no basis to assert what realizations we might have have.

I believe, for reasons of finite resources requiring us to work or sleep or spend times with friends and family, that both of us independently have come to the conclusion that your immediate education is not our number one priority at all hours of the day and night.

I see that you have removed my name from this sentence on the basis of data.

--
So what have we learned?
If $$f(x_1, ..., x_n)$$ is a function then the total derivative with respect to one of it's inputs
$$\frac{d \quad}{d x_j} f = \sum_{i=1}^n \frac{\partial f}{\partial x_i} \times \frac{d x_i}{d x_j} = \frac{\partial f}{\partial x_j} + \sum_{i \neq j } \frac{\partial f}{\partial x_i} \times \frac{d x_i}{d x_j} $$
And that this looks like the inner product of $$\left( \vec{\nabla} f \right) \cdot \begin{pmatrix} \frac{d x_i}{d x_1} \\ \vdots \\ \frac{d x_i}{d x_{j-1}} \\ \rule[-1em]{0pt}{25em} 1 \\ \rule[-1em]{0pt}{25em} \frac{d x_i}{d x_{j+1}} \\ \vdots \\ \frac{d x_i}{d x_n} \end{pmatrix} =\begin{pmatrix} \rule[-10em]{0pt}{25em} \frac{\partial f}{\partial x_1} \\ \vdots \\ \rule[-10em]{0pt}{25em} \frac{\partial f}{\partial x_{j-1}} \\ \rule[-10em]{0pt}{25em} \frac{\partial f}{\partial x_j} \\ \rule[-10em]{0pt}{25em} \frac{\partial f}{\partial x_{j+1}} \\ \vdots \\ \rule[-10em]{0pt}{25em} \frac{\partial f}{\partial x_n} \end{pmatrix} \cdot \begin{pmatrix} \rule[-10em]{0pt}{25em} \frac{d x_i}{d x_1} \\ \vdots \\ \rule[-10em]{0pt}{25em} \frac{d x_i}{d x_{j-1}} \\ \rule[-10em]{0pt}{25em} 1 \\ \rule[-10em]{0pt}{25em} \frac{d x_i}{d x_{j+1}} \\ \vdots \\ \rule[-10em]{0pt}{25em} \frac{d x_i}{d x_n} \end{pmatrix} $$

But where post 18 jumps the shark is where it goes from talking about an abstract function of variables, to a concrete function where the only variables seen are $$\theta$$ and $$x$$. There is no formal dependency on u and v in that three-part sum.

In $$f(x,y,z) = xyz$$, $$\frac{d f}{d x} = \frac{d \quad}{d x} xyz = yz + xz \frac{dy}{dx} + xy \frac{dz}{dy}$$ but if you change the function under discussion to $$f = 3xt$$ I don't have any logical basis to think you are talking about $$f(x,t,3)$$ or $$f(x,3t,1)$$. Nevertheless, the partial derivative of 3xt with respect to x is the same no matter how this expression relates to the original f. $$\frac{\partial \quad}{\partial x} 3xt = 3t$$. Math is both rigid and fragile like that so the speaker has to be precise.

The term partial in "partial derivative" does not mean you have carte blanche to stop the process of calculating the derivative at any intermediate step. It means that the derivative is only with repect to changing one variable, and holding the others constant. When you confuse matters by first saying $$f(\theta,u,v) = 3 \theta + u + v$$ and then talking about the case which was constrained to $$u = \sin^2 \theta, \; v = \ln x$$ (this is hypothetical, because post 18 isn't this explicit) then you are no longer talking about the same f. This new function, for which I shall use a new name, is $$g(\theta, x) = 3 \theta + \sin^2 \theta + \ln x$$.

As should be clear, the partial derivatives of f and g look nothing alike.
$$\frac{\partial f}{\partial \theta} = 3 , \; \frac{\partial f}{\partial u} = 1 , \; \frac{\partial f}{\partial v} = 1 , \; \frac{\partial f}{\partial x} = 0 \\ \frac{\partial g}{\partial \theta} = 3 + 2 \sin \theta \, \cos \theta , \; \frac{\partial g}{\partial u} = 0 , \; \frac{\partial g}{\partial v} = 0 , \; \frac{\partial g}{\partial x} = x^{\tiny -1} \\ \frac{\partial u}{\partial \theta} = 2 \sin \theta \, \cos \theta , \; \frac{\partial u}{\partial u} = 1 , \; \frac{\partial u}{\partial v} = 0 , \; \frac{\partial u}{\partial x} = 0 \\ \frac{\partial v}{\partial \theta} = 0 , \; \frac{\partial v}{\partial u} = 0 , \; \frac{\partial v}{\partial v} = 1 , \; \frac{\partial v}{\partial x} = \frac{1}{x} $$

Post 18 is fundamentally flawed when it skips steps of defining u and v and when it skipped the step of defining f the way you meant it defined. Because of these miscommunications, post 18 is indefensibly wrong, because you flipflop between a definition of f that is written for us and a definition that exists only in your head in some nebulous form and would not begin to be expressed for us until post 27. But instead of fixing the problem, you dug yourself in deeper with misstating the definition of partial differentiation and perversely ignoring the obvious theta-dependency of the second term.

Partial differentiation requires a formal expression defined over a certain set of variables. When you write a nebulous expression like $$f = 3 \theta + \sin^2 \theta + \ln x$$ then your readers assume that $$theta$$ and $$x$$, being otherwise unexplained, are among the variables. Strictly formal rules (the sum rule, the product rule, the law of composition, the chain rule, ...) allow us to process the expression. Alternately, you can go the route AlphaNumeric kindly went and explicitly compute the partial derivative.

But just as f and g had different definitions in your head (but were both written as f in post 18) so do f and g have different definitions of parameter space. This is not surprising because if $$f(\theta,u,v)$$ has a 3-dimensional parameter space, the constraint $$u = \sin^2 \theta$$ reduces it to a 2-dimensional parameter space of independent variables $$\theta$$ and v. You have eliminated all the posibilities to consider when $$u /neq \sin^2 \theta$$ and this is part of the reason why $$f(\theta,u,v)$$ cannot be considered identical to $$g(\theta, x)$$ and if f and g are not identical, there is no reason to think that there partial derivatives must be.

 

[James R]

I've just been reading back a bit. As detailed in post #174, it seems Tach has made another laughable error. Now, as usual, instead of admitting he made a silly mistake, he is going to great lengths to try to cover it up.

Don't you realise, Tach, that if you just admitted your many errors in the first place, you wouldn't have this desperate clambering for status all the time? If you make a mistake, own it and move on. This denial of your own imperfections is a sign of a deep lack of confidence and immaturity.

 

[Trippy]

A graph of z = x[sup]2[/sup] + xy + y[sup]2[/sup].

See, to me, if z=f(x,y) I would compute the partial derivatives by treating it as the following.

Rightly or wrongly

I would derive $$\frac{\partial z}{\partial x}$$ by treating it as f[sub]y[/sub](x)=x[sup]2[/sup] + ax +b
and $$\frac{\partial z}{\partial y}$$ by treating it as f[sub]x[/sub](y)=y[sup]2[/sup] + ay +b

 

[AlphaNumeric]

Because this is NOT the way the function is presented. If someone was so perverse to define $$T=\frac{m u^2}{2}$$ with $$u(\dot {q})=\dot {q}$$ only THEN $$\frac{\partial T}{\partial \dot {q}}=0$$.

It isn't , but you really need to be willing to listen.

See above, it is really simple.

So $$\partial_{\theta}\sin^{2}\theta$$ isn't zero, yet you said in post 18 it is. Sorry, you've just massively contradicted yourself.

Also, you continue to fail to address the potential term and by redefining the coordinate you're being dishonest because you're moving the goal post. In post 18 you take the $$\theta$$ derivative of a theta dependent function, namely $$\sin^{2}\theta$$ and you say it's zero. You have said this happens for any function of the variable. The variable squared is a function of the variable, just like sin is. You're contradicting yourself.

In post 18 you say that $$f = 3\theta + \sin^{2}\theta + \ln x$$ gives $$\partial_{\theta}f = 3$$. You've just said $$\partial_{\theta}\sin^{2}\theta \neq 0$$. Derivatives are linear operators, so $$\partial_{x}(g+h) = \partial_{x}g + \partial_{x}h$$. Let's apply this to your f, $$\partial_{\theta}(3\theta + \sin^{2}\theta + \ln x) = 3\partial_{\theta}\theta + \partial_{\theta}\sin^{2}\theta} + \partial_{x}\ln x$$. The last term goes and the first term is trivial so we get $$\partial_{\theta}f = 3 + \partial_{\theta}\sin^{2}\theta$$. You said in post 18, which you reference so often, that the answer is 3, so this is only possible if $$\partial_{\theta}\sin^{2}\theta = 0$$. Now you're saying that isn't the case.

How can you not see you have contradicted yourself?

Not only have I given the definition of the partial derivative and shown it doesn't agree with you (and you haven't yet actually shown where I was mistaken in that derivation), as well as used standard examples from mechanics but now I've used your own posts!

Look, the fact that so many people with advanced degrees in math miss this simple thing is nothing short of amazing. The fact that six of you (AN, you, rpenner, przyk, Guest254, prometheus) argue(d) against only one of me doesn't make you right and me wrong.

No, but it would make most rational people stop and think for a moment. Remember, most of the people you just listed use partial and total derivatives a lot. This last fortnight I've been doing thermodynamics, classical dynamics and stochastic processes, all of which have various derivative concepts in them and keeping track of them is very important (god I ****in' hate it in thermodynamics!). Anyone who has done any classical mechanics or quantum field theory or general relativity will have had similar experiences, which includes all of the people you've listed.

You keep pointing at the book or post 18 but you ignore how people have said "Yes, that equation is correct" but then gone on to explain how you're misapplying it or being disingenuous. Now you've nailed your trousers to the mast by saying in post 18 that $$\partial_{\theta}\sin^{2}\theta = 0$$ (unless you believe derivatives aren't linear operators?) and also said it isn't.

I can see this thread isn't going to go anywhere further than it is at the moment. You've failed so completely and utterly to grasp this stuff, you've been shown to be mistaken many different ways and you've also been a hypocrite for complaining about talking down to people when you're doing precisely that to others. Sorry Tach but you're now in the same category as Motor Daddy or Geist (or the long defunct member Jack_) IMO. You've put your foot in it a few times in a small way, which is what I thought you'd done when you first had a go at the OP for saying $$\partial_{x}$$ might be a vector element in some vector space (a mistake I haven't seen you acknowledge yet) but recently you've been sparking more and more lengthy, down hill 'discussions' like this one and you've been moving more and more into the realm of disruptive crank. Sure, you might know more physics/maths than typical for such a person but unfortunately you also seem to be suffering from the same issue as Jack_ or chinglu, an unrealistic view of your knowledge. I don't know if you do physics/maths professionally but my gut says no. You'd be less inclined to over estimate yourself if you were doing actual problems, you'd have a better sense of what you do or don't know. That's why the comments from those of us who are researchers are worth listening to, not because we have 'PhD' after our names but because for us it's trial by fire. Without the constant tests it might be all too easy to fall into the mindset of people like Farsight, ie having all the answers but never addressing actual problems. I fear your "Look at post 18! Look at the book!" auto-responses and inability to formulate proper informed discussion in response to other posts is a sign that you've fallen into a similar (but not quite as deep) intellectual hole.

To everyone else I'm wondering whether people want this thread to continue. It's currently not a flame war but we are going round in circles with Tach. If people are content to go around and around for some more time, hoping Tach at some point actually tries to calculate something like the definition of the partial derivative applied to his function, then fine. If you think enough is enough then say so and when I get up in the morning I'll check the thread and see which way the wind is blowing.

 

[arfa brane]

I would derive $$\frac{\partial z}{\partial x}$$ by treating it as f[sub]y[/sub](x)=x[sup]2[/sup] + ax +b
and $$\frac{\partial z}{\partial y}$$ by treating it as f[sub]x[/sub](y)=y[sup]2[/sup] + ay +b

Hang on, if you're substituting for y in the first equation, then a = b since y is constant. Otherwise are you saying y can have two values?