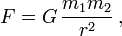Well, here's my take on it, starting from the ground up as a humble English peasant living in medieval ages and paying taxes in gold to the local Baron:
I have a simple balance scale consisting of a lever hanging by a rope attached at the middle (the "fulcrum point") to some support structure which holds it up. I attach light straw buckets to each end of the rod (both buckets being roughly equal in size, shape and material) and place some items in each bucket (perhaps apples in one bucket, eggs in the other). I add enough items to each until there's a balance, and note that both buckets have the same qualitative weight when I try to lift them by hand, indicating there's some sort of relationship between this balance and what I feel when I try to lift each load.
Now I start to play around a bit. I start with two balanced buckets (one with apples, one with eggs), swap their places on the balance rod, and notice that they still remain balanced. At this point, I decide there must be something equivalent about the contents of the two buckets, and I choose to call this mysterious equivalent property "mass". For instance, I can show that if a basket of apples balances with a basket of eggs, and that same basket of eggs balances with a basket of oranges, then the baskets of apples and oranges will also balance when I put them on my crude scale. I can get even fancier and show that if I have four buckets A, B, C and D, for instance, and the contents of A balance the contents of C while the contents of B balance with the contents of D, then combining the contents of A and B on one side, C and D on the other side, still leads to a net balance, suggesting the masses on both sides simply add.
We have a couple of final steps before we can conclusively establish that there's some internal property of matter (mass) which is leading to this gravitational balance. If I have two balanced buckets equal distances from the fulcrum on which my scale hangs, and move one of the buckets further away, I notice the balance will start leaning in the direction of the bucket I moved further away, just like what happens on a seesaw. I get the same lean in the opposite direction if I do the same thing to the other bucket instead, and finally if I move both buckets an equal distance, the net balance remains unchanged. So at this point I'm a little confused- I thought I had a nice scheme for defining the mass of something based on what it balanced with, now I see that balance also depends on the distances of the buckets from the fulcrum. Hmmm... Well, for starters, I note that if I have two buckets which balance at equal distances, then the direction and rate of leaning depend only on whether I shift around one bucket or the other and by how much, and it does not depend on the particular contents of these buckets. Maybe then I can still argue that these buckets contain equal masses, and the leaning of the balance has something to do with not having the buckets equally spaced from the fulcrum.
So I decide to go back to my original scheme as a starting point, and weigh out three baskets of apples so they all balance in pairs when placed at equal distances from the fulcrum, i.e. according to my original scheme they all have equal mass. I place two buckets of apples at one end, and one bucket at the other. Naturally, the balance immediately starts to lean towards the side with more apples, but then I do something clever: I notice that if I double the distance of the lighter load from the fulcrum, I've once again achieved a balance! Same thing if I have three buckets of apples on one side and one bucket on the other, each bucket having been measured in advance to be equal in mass- now if I triple the distance instead of doubling it, I've once again restored a balance. So at long last, I can explain all the results of these tests with two simple assertions:
- All objects have an intrinsic quantity called "mass". The mass of two objects combined is the sum of their individual masses.
- If I have masses m[sub]1[/sub] and m[sub]2[/sub] placed distances L[sub]1[/sub] and L[sub]2[/sub] from the fulcrum, respectively, then these masses balance when m[sub]1[/sub]L[sub]1[/sub]=m[sub]2[/sub]L[sub]2[/sub]
The second principle was originally discovered by Archimedes (some call it the "principle of torsion balance"). He more or less worked along the line of reasoning I presented above, but English peasants tended to be rather ignorant of ancient Greek advances, so we can be a little forgiving here. And finally, once I've played around a bit, have thoroughly tested and established my notions of mass and torsion balance, I come to the realization that my buckets themselves have a bit of mass, and I should have accounted for that in the first place when setting up my measurements, but it didn't matter at the time because the buckets were light compared to their contents, and each bucket tends to weigh a similar amount in the first place, further hiding this fact. This is an easy correction to make, and all the tests and experiments can be redone now with ease while taking this into account.
Then along comes a guy like Newton or Galileo, and starts hooking weights up to pulleys and having those pulleys drag smooth, flat blocks of stone across horizontal tables. If the tables and stones are smooth enough, you can note that the acceleration of these stones is proportional to the weight you attach to your pulley (we can define this weight as "gravitational force"), and inversely proportional to the mass of the stone itself. Thus, you can define a system of units, define what a force is and what it means for two forces to be "equal" or what it means for one force to be some multiple of another, and thus establish a law such as F=ma, which then allows you to extend your concepts to things like pendulums, springs and planetary orbits.
Note: as a non-historical alternative, you could so a similar set of tests with springs as a starting point, establish concepts of force and mass, and then show it applies equally well to problems involving weights and gravity. Historically, the idea of mass was first defined in terms of how much it weighs when you lift it, and all they had to do was pick some object to label as a kilogram or a pound or what have you, against which everything else would then be compared.