The Monty Hall Problem Revisited

[gmilam]

But here's the converse.

You walk into the room. A previous person has already chosen door 1. Door 3 has been opened and contains a goat. The previous person then leaves.

Now you have two doors to pick from. You never had three doors. Which do YOU choose?

In this case, you do indeed have a 50/50 chance.

 

[billvon]

In this case, you do indeed have a 50/50 chance.

What is the difference between the two cases? Why does it matter who makes the decision?

 

[phyti]

TheVat;

Sigh. You need to acquaint yourself with Bayes theorem. It really really helps in understanding the seeming counterintuitive correct answer. Google bayes monty hall.

Sigh Fi. May the farce be with you.
No need to make a simple problem overly complicated.
----------------------------------------------
Anyone;
No door contains 1/3 car. The abstract values in math don't always correspond to something in the real world. The census reports the average family has 2.3 children, but no one expects to find .3 child in any household.
Enter truth tables.
Possibility is closer to reality. In the post 28 example, the host knows the location of the car, and his knowledge is {1, 0, 0}. The player does not know the location of any prize and his knowledge is {?, ?, ?}, ? meaning no knowledge.
As a substitute for knowledge, math distributes the probability of 1 for (the set of 3 doors) uniformly as 1/3 for each door.
The host has now revealed 1 door has no car. That informs the player of where the car is NOT located, and alters the player's knowledge to {?, ?, 0} or {?, 0, ?}. The game has changed from a set of 3 to a set of 2 closed doors for the player's 2nd choice since 1 door has been eliminated. The player can still only make a random guess. One guess wins a car, one guess wins a goat. Measure of success is (win a car)/(games played)=1/2. To repeat what you may have missed,
there are not 3 ways to choose 1 of 2 things.

In logic (x AND y) is different from (x OR y).
When the car is behind door 1, the host can reveal door 2 OR door 3, but NOT both in the same game.

1. Savant considered both as 1 game, a goat is a goat. Since there are 2 goats existing simultaneously, they require different identities, 1 & 2, Maude & Claude, etc. The example in post 28 uses 3 distinct prizes. If it helps, substitute g1 and g2 for a and b.
2. Savant also thought the 2/3 probability for the set of 2 doors not chosen, could be transferred to the one remaining after opening the other, which is false.
p=probability of location, which depends on number of doors.
doors________ p
1 2 3 4 5 6__ 1/6
1 2 3 4 5____ 1/5
1 2 3 4______ 1/4
1 2 3________ 1/3
1 2 __________1/2
1____________ 1/1

There are 6 possible arrangements of prizes (left) in my table, but 8 possible outcomes (right). The difference is due to participation of the host.

A simulation based on Savant's erroneous basis will obviously reproduce her results. That does not prove her explanation is correct.

 

[DaveC426913]

No need to make a simple problem overly complicated.

So what is your verdict? What's the TL;DR?
Better to switch or no?

 

[Sarkus]

What is the difference between the two cases? Why does it matter who makes the decision?

It doesn't matter who makes the decision. It matters when you make the choice, and the options you are given at that time.

To me it's all about what you know.

In the original 3 door problem there is a prize behind one door. So you pick 1 knowing that you have a 1/3 chance of being correct. Therefore there is a 2/3 chance that the prize is behind one of the other two doors. Hopefully everyone accepts this so far?

What you also know is that at least one of those other two doors does not contain a prize, right? You don't know which of them doesn't, but you do know that at least one doesn't.
With me so far?

Okay, so the host opens one of those 2 doors and shows no prize. Has your knowledge changed with regard how many of those doors doesn't contain a prize? No. You knew it was at least one that didn't, and now you still know at least one doesn't. Sothere has been no change to your information with regard whether the prize is behind the door you initially chose, or behind one of the other two.

Since your information hasn't changed, your odds haven't changed. I.e. your initial choice still has 1/3 of being correct, or 2/3 of being wrong.
The other two doors together still have 2/3 of being correct.

So would you swap? Your original choice had only 1/3 chance of being correct. It still has only 1/3.

You should swap. Every time. At least based on the odds.

 

[gmilam]

What is the difference between the two cases? Why does it matter who makes the decision?

I was heading out the door to the theater and made a flash decision. I was wrong. The original choice still has a 1/3 chance of being correct and the remaining door, after Monty eliminates a zonk, still has a 2/3 chance of being the prize. Sarkus explains it nicely.

I would add that 2 out of 3 times, the prize is behind one of Monty's doors. But 3 out of 3 times Monty eliminates a zonk door. Monty NEVER eliminates the prize door.

 

[phyti]

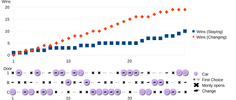
Player 1st choice is door 1.



First diagram shows all possible choices when restricting the host to opening only a door not containing a car 'c'.

If c is behind door 1, host has 2 games per arrangement.

If c is not behind door 1, host has 1 game per arrangement.

Comparing door 1 column to 'op' column verifies the win car ratio of 4/8=1/2.



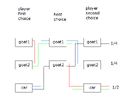
Second diagram shows all possible choices for player and host emphasizing host restriction to opening only a door not containing a car.

Follow the colored paths, which verifies the win car ratio of 2/4=1/2.



In all cases, the host using a left to right rule to choose 1 of 2 doors is equivalent to randomly choosing, for a large number of games. No different than flipping a coin.

 

[gmilam]

Forget the host eliminating an option. Suppose that the host said, "You can swap your door for the other two doors." Which would you take? Because for all practical purposes, that's what your choice is.

 

[phyti]

So what is your verdict? What's the TL;DR?
Better to switch or no?

If you compare, stay vs switching, there is no difference. That's why the win ratio s 1/2 for both.
From post 28: The logic of the game, with the player never knowing where the car is located until after their 2nd choice, precludes them from defining a basis for a strategy. It's always a random guess

gmilam:
The host can only offer door 1 and 'op' the remaining closed door for the player's 2nd guess. Examine the above graphics.

Will anyone of those who thought they were revealing a proof of Savant's explanation, admit they were wrong?
Probably not!
Marilyn Savant is approx. 80, and retired. As a senior, your priorities change. What was important in the past is not today.

 

[DaveC426913]

If you compare, stay vs switching, there is no difference.

Well, the data seems to suggest otherwise.

 

[gmilam]

If you compare, stay vs switching, there is no difference. That's why the win ratio s 1/2 for both.
From post 28: The logic of the game, with the player never knowing where the car is located until after their 2nd choice, precludes them from defining a basis for a strategy. It's always a random guess

gmilam:
The host can only offer door 1 and 'op' the remaining closed door for the player's 2nd guess. Examine the above graphics.

Will anyone of those who thought they were revealing a proof of Savant's explanation, admit they were wrong?
Probably not!
Marilyn Savant is approx. 80, and retired. As a senior, your priorities change. What was important in the past is not today.

We all agree that 1 out of 3 times you will pick the prize door. Therefore, 2 out of 3 times you picked the wrong door and are better off switching.

 

[DaveC426913]

We all agree that 1 out of 3 times you will pick the prize door. Therefore, 2 out of 3 times you picked the wrong door and are better off switching.

That logic isn't sufficient or exhaustive. (It my be true, but it doesn't explain why it might be true.)

We all agree that 1 out of 3 times you will pick the prize door.

True.

Therefore, 2 out of 3 times you picked the wrong door

True.

and are better off switching.

This does not follow immediately. There is some logic to be done to show that switching gives you better odds.

 

[gmilam]

That logic isn't sufficient or exhaustive. (It my be true, but it doesn't explain why it might be true.)

True.

True.

This does not follow immediately. There is some logic to be done to show that switching gives you better odds.

2 out of 3 times the prize is behind one of Monty's doors.

3 out of 3 times Monty eliminates a zonk. Monty never eliminates the prize.

 

[gmilam]

MontyEliminatesOneOfTwoDoors(ThisDoor, ThatDoor) {
if (ThisDoor = PrizeDoor) {
open ThatDoor;
PrizeIsBehindUnselectedDoor = *true; }
elseif (ThatDoor = PrizeDoor) {
open ThisDoor;
PrizeIsBehindUnselectedDoor = *true;}
else {
open EitherDoor;
PrizeIsBehindUnselectedDoor = *false;}
endif';
}

 

[phyti]

This may be more convincing since it is from Savant's viewpoint and shows how subtle her mistakes are.

The slightly simplified table below was used in Marilyn Savant's 1990 reply to Craig Whitaker's question of strategy, 'to stay with 1st choice or switch to other door for the 2nd choice'.

1. Her response to one of her critics.

"My original answer is correct. But first, let me explain why your answer is wrong. The winning odds of 1/3 on the first choice can’t go up to 1/2 just because the host opens a losing door".

2. Her instructions.

"The benefits of switching are readily proven by playing through the six games that exhaust all the possibilities. For the first three games, you choose #1 and "switch" each time, for the second three games, you choose #1 and "stay" each time, and the host always opens a loser. Here are the results."

g	d1	d2	d3	switch	stay
1	auto	goat	goat	lose
2	goat	auto	goat	win
3	goat	goat	auto	win
4	auto	goat	goat		win
5	goat	auto	goat		lose
6	goat	goat	auto		lose

3. Her conclusion.

"When you switch, you win 2/3 of the time and lose 1/3, but when you don’t switch, you only win 1/3 of the time and lose 2/3."



Her response in (1.) is false. The open door reveals (no auto), thus it is no longer a possible location. The probability (1 for the set of doors) is now shared equally for 2 doors.

In game 1, the host reveals a goat behind a door, but which goat?

She considers either goat1 or goat2 as one game, which is false.

The host can only open 1 door, since opening 2 doors would end the game.

Her claim that six games exhaust all the possibilities in (2.) is also false.

If games 1 and 4 are corrected for 2 goats, 'switch' gains 1 lose, and 'stay' gains 1 win.

That makes the results for each equal, with no advantage.

ref:

Marilyn vos Savant

web.archive.org

 

[gmilam]

It's hard to let go of that initial impression. I fell for it 30 years ago when it was first published, and I fell for it again last week when billvon altered it slightly.

Let's try a different approach... There's a 100% chance that Monty opens 1 door.

Option1 - Player selects door for goat a:
There's a 0% chance Monty opens the door eliminating the car. And a 100% chance Monty opens the door for goat b.

Option 2 - Player selects door for goat b:
There's a 0% chance Monty opens the door eliminating the car. And a 100% chance Monty opens the door for goat a.

Option 3 - on the outside chance that the player selected the car:
There's a 50% chance Monty opens the door for goat a. And a 50% chance Monty opens the door for goat b.

 

[Sarkus]

This does not follow immediately. There is some logic to be done to show that switching gives you better odds.

Okay.
Close your eyes.

Do you accept that, with a car behind one door, and goats behind the other two, you have a 1/3 chance of picking the car?

Do you accept that, of the two doors you didn't pick, at least one of them will have a goat behind it?

Now, with your eyes still closed, Monty opens a door with a goat behind it. (The audience tell you that this is what he has done)

All Monty has done is reveal what you already knew, that there was at least one goat behind the doors you didn't pick. Do you accept this so far?

So your knowledge hasn't changed, has it?

Your initial pick had 1/3 chance. There was therefore 2/3 chance it was behind either of the other two. You also knew that at least one of those other two has a goat behind it.
You still know all those things, and nothing has changed.

So why would you think your odds of winning with your original pick have improved from 1/3 to 1/2?



Here's another way of looking at it.
Imagine there are 52 playing cards faced down. I know which one the Ace of Spades is, but you don't.

I ask you to pick the Ace of Spades. You have a 1/52 chance, but you keep the card faced down for now .

I then turn over 50 cards that I know are not the Ace of Spades. So now there are just two cards faced down: the one you picked, and the one I've left out of the other 51.

Do you swap?
Or are people going to cling to the idea that the odds are now 50:50??

 

[Sarkus]

Player 1st choice is door 1.



First diagram shows all possible choices when restricting the host to opening only a door not containing a car 'c'.

If c is behind door 1, host has 2 games per arrangement.

If c is not behind door 1, host has 1 game per arrangement.

Comparing door 1 column to 'op' column verifies the win car ratio of 4/8=1/2.

Your mistake is assuming each outcome (op) is equally weighted. They're not.

Each game has the same weight. So choosing a, b, or c (column 1) each have a weight of 1.
The outputs of those individual games must thus total that same weight. If there are four outputs, each output has weight of 0.25. If there are 2 possible outputs, each has weighting of 0.5.
So column 1 has a total weight of 3, and column "op" should have a weight of 3.
You are giving "op" a weight of 4.

Once you correct for this mistake, your analysis will give you the correct result, that swapping increases your odds from 1/3 to 2/3.

 

[DaveC426913]

Okay.
Close your eyes.

OK. But you have changed the parameters of the scenario.

Do you accept that, with a car behind one door, and goats behind the other two, you have a 1/3 chance of picking the car?

Do you accept that, of the two doors you didn't pick, at least one of them will have a goat behind it?

Now, with your eyes still closed, Monty opens a door with a goat behind it. (The audience tell you that this is what he has done)

Of what use is asking me if I have more information if you have just eliminated one channel of information?

All Monty has done is reveal what you already knew, that there was at least one goat behind the doors you didn't pick. Do you accept this so far?

So your knowledge hasn't changed, has it?

Yes it has. I now know which door not to pick (if my eyes are open).

So why would you think your odds of winning with your original pick have improved ...

Because that is what the data shows.

 

[gmilam]

Your chart shows that you win twice as often if you switch.