Why are you asking me to prove your case?
I am not asking you since I know you will never put down the math. I am asking przyk.
Why are you asking me to prove your case?
Consider the worldlines of the rim ends of opposite spokes, horizontal at t'=0:
$$x_1' = -R.cos(\omega t') \\
y_1'-R = R.sin(\omega t')$$
$$x2' = R.cos(\omega t') \\
y_2'-R = -R.sin(\omega t')$$
This is completely wrong. I did acknowledge that (I'm not sure I really agree with the terminology, but let's go with it). In fact it should have been clear I was well aware of this way back in my [POST=2848590]first post[/POST] in this thread, when I asserted that most of the mass would be in the top half in the ground frame, and from my subsequent elaboration at the end of [POST=2848712]post #59[/POST].But what both you and przyk fail to acknowledge is that the notion of what is "upper half" is frame dependent.
First of all, stones and glass houses: you have never shown any calculations. Your single lazy [POST=2848455]attempt[/POST] at a derivation contained not one but two conceptual errors.You made no attempt, przyk made a sketch that I have shown to contain an invalid parametrization of the length of the halves as a function of the arc length.
That's an odd comment since I'm the one that posed the question under discussion.You know, if you don't even understand the subject of the debate after so many posts...
No.I said "gravitational effects" as in "differences" between the "upper" and "lower" half. Do you think that there are any differences for an observer located in the center of the wheel?
You tell me, since I never said such differences would appear.If there aren't any, why would such differences appear for a moving observer?
No, it is you who is claiming that the fact the upper half has more energy would imply "gravitational effects". I do not take your word for it that "the effects increase with the relative speed between the observer and the axle". So, derivation or reference please.This is what your approach claims, so I am asking you to prove it.
Second, you have not "shown" that my parameterisation was invalid, you merely said it was in a pathetic attempt to redefine the problem.
But you know what, let's forget that for a second, because your strawman backfires spectacularly. Let's say we do define the top half "invariantly", meaning that the collection of wheel elements constituting the "top half" at some instant in the ground frame is the same as the collection of wheel elements in the top half at some "corresponding" instant in the axle frame.
Then the approach you tried in [POST=2848455]post #51[/POST] does become valid (with the correction $$p_{\mathrm{upper}} = - p_{\mathrm{lower}}$$), because it applies to an invariantly defined collection of wheel elements. So setting $$E \equiv E_{\mathrm{upper}} = E_{\mathrm{lower}}$$ and $$p \equiv p_{\mathrm{upper}} = - p_{\mathrm{lower}}$$, you find
$$
\begin{align}
E'_{\mathrm{upper}} &= \gamma (E + pv) \,, \\
E'_{\mathrm{lower}} &= \gamma (E - pv) \,.
\end{align}
$$
which are clearly different unless $$p = 0$$ (i.e. a non-rotating wheel).
Whoops.
Yeah, nasty thread.
Just consider the concept - a tank, proper length L driving along the road at speed v.
The tank's track runs forward and back along the length of the tank, around infinitesimal driving wheels at each end.
The bottom half of the track is in contact with the road.
In the tank frame, the top and bottom halves of the track are both moving at speed v.
The track's total proper length is $$2\gamma L$$.
In the road frame, the bottom half of the track is at rest, and has proper length $$L/\gamma$$.
Since track density is proportional to proper length, it is clear that in the road frame less than half the track's mass is in the bottom half.
...because there is no PROOF to that. Just some armwaving and no math. Neither of you calculated the mass of the "upper" half. We can't even agree what "upper" half is. Put up a calculation and we'll talk.
przyk did no calculation, he showed a generic formula that proves nothing.
That is false. For the third time, you need to use the transformed (aberrated) line, i.e. the inclined line that is the transformation of the horizontal line passing through the axle.
The aberration of the distribution of the rim is inherent in the thread from the very first post, so you 'pointing it out' is kind of redundant.
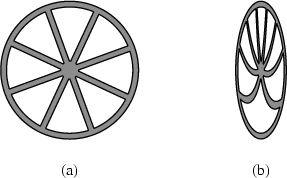
As late as post 48, you were still questioning whether the transformed midline would be S-shaped or U-shaped.
The wheel will not appear like an eclipse. There is a funny combination of light delay effects which h means the wheel will remain looking like a circle. Its named after Penrose and someone else. Length contraction happens but visually a second opposite effect conspires to cancel it in the case of circles and spheres, not anything else. Its to do with how the boost is like a complex rotation in time. Ill Google when I am not using a phone to post.
However, since the hypothetical involved here, goes far beyond any pratical real situation, how is it possible to know with any certainty what impact frame dragging might play? The hypothetical involves conditions that cannot exist, except within a hypothetical, science fiction or one's imagination. At least within the context of current knowledge and technologies.
Whoa Przyk, to be fair to Tach, I don't think anyone actually thinks the paradoxical gravitational effects would occur based upon who is making the observation. My question is simply, how does the framework avoid them from occurring? Did you see my question's reformulation 2 posts ago?
(That being said, if I had my way Tach would be completely barred from this discussion. Arrogant condescension, cherry picking arguments, nit-picking irrelevancies, rewriting history and being plain wrong is a bad combination)
Yes, looks right now.
Except that a problem surfaces: if you put up a "fence" of height R , more than half the spokes will be visible above the "fence". This doesn't seem right. This is where this thread started from. So, something is terribly wrong with this "picture".
Yes, this track around a tank is the same concept! But it is a lot better because the effects of terrell penrose rotation won't affect it so neatly, or that is my first impression.
The proof is there, but it is not a mathematical proof!
Me, przyk, RJBeery, and pete all see it while you for the longest time are arguing against it. Are you really not convinced by simple word proofs based on common sense?
The aberrated mid-line is a red herring; the main focus is the way the wheel appears to an outside observer, and what gravitational effects it will have on an outside observer.
So, while we are talking about aberration, and were from the very beginning, it is not 100% that the wheel will look distorted when observed from a side view (where the wheel is in the plane of the monitor):
In addition to this, the movies that I have shown also support that a relativistic wheel will not look distorted from a side view, because of some other relativistic spookiness.
Granted, I put a lot of faith in these videos. From the videos it seems that a wheel spinning at relativistic speeds will look differently distorted depending on what angle it is viewed from.
This does not defeat the purpose of the argument, which is to show that the center of mass of the wheel/tread will shift without any apparent force.
Hello? What are atoms? They are nuclei which are orbited by electrons in circular paths.. right?
That is not true, it can exist, and it can even exist on earth.
While a wheel spinning at relativistic speeds cannot exist, because of the relativistic forces, it can exist in another case.
Take the tank-tread. The tank tread is accelerated to 30 m/s. Then, the entire tank is accelerated to c - (1 m/s). The thread on the tank will not snap because that would mean different rules in the frame of the tank. But, to us it will still appear as if most of the mass was either in the lower or upper halves.
On earth, it can exist in a particle accelerator. Hello? What are atoms? They are nuclei which are orbited by electrons in circular paths.. right?
No, you called it "invalid", asserting that it was "not invariant", which is not an argument against it. This is pathetic revisionism. Now that you're cornered, suddently you're trying to tell everyone what the problem really was, even after RJ, the person who brought it up, corrected you about that.Sure I showed you that the parametrisation is invalid
No, it follows from the way everyone, except you, is defining the top and bottom halves of the wheel. The silhouette of the wheel in the ground frame is a length contracted ellipse with mirror symmetry about the horizontal axis, so each half gets half the perimeter. It's really not complicated.you blindly assume that each half maps in a L length interval (one into [0,L] and the other one into [L,2L]).
When it's you who doesn't understand the problem everyone else is discussing, you are hardly in a position to tell anyone else what they're doing is backwards.But this is precisely what you got backwards and you continue to get backwards.
Are you saying you're just defining the "top" half as the collection of wheel elements that happened to be at the top of the wheel initially in the axle frame? Does the "top half" of the wheel periodically touch the ground? If so, can you explain how in the world you got that from [POST=2847579]RJ's post that started all this[/POST]?What I have been telling you is that the separation between the two "halves" is dynamic. Its equation is the equation of the spoke corresponding to $$\phi_i=0$$.
Tach said:Except that a problem surfaces: if you put up a "fence" of height R , more than half the spokes will be visible above the "fence". This doesn't seem right. This is where this thread started from. So, something is terribly wrong with this "picture".
Thanks for the link. I'd forgotten about that thread. Classic Tach.Here, remember?
...especially where it describes this image (visual appearance of the rolling wheel in the ground frame):Then, you have to deal with the very disturbing issue that , if you covered half the wheel with a fence of height R, you would be seeing 6 spokes (not 4) above the fence. I pointed out this to you twice.


No, Tach, we're quite clear on what is frame dependent.But what both you and przyk fail to acknowledge is that the notion of what is "upper half" is frame dependent.
No, I've never said that you can get gravitational effects by moving the wheel.Tach said:You mean that you still maintain that you can get gravitational effects by moving by the wheel? And your answer is just "GR spookiness"?
Correct, bearing in mind that we're talking about the geometric upper half in the moving frame.Well , for one, you all claim that the "upper half" of the wheel has more energy (kinetic, total) than the "lower half".
Do you have any calculations to support that assertion?So, since total energy does gravitate, it follows that any moving frame could detect this disparity while the axle frame will obviously not detect anything.
It seems to me Przyk's integral is explicitly about that particular claim. Perhaps you didn't read it properly, so here it is again:NO. None of you posted a formal calculation supporting this claim.
Why?I will post my calculation AFTER you post yours supporting the opposite claim.
Your parametrization is for spokes that are vertical at $$t'=0, \phi=0, \phi=\pi$$Tach said:Yes, you are right. I get that the spokes are on the same side of the diameter, though my math is different since I have the parametrization of x and you the reverse of yours:
$$x'=R sin (\omega t' +\phi)$$
$$y'=R cos (\omega t' +\phi)$$
leading to the exact equation of the spokes given early in the thread:
$$y-R=\gamma (x-Vt) ctan[\omega \gamma (t-Vx/c^2)+\phi_i ]$$
t=0 results into:
$$y-R=\gamma x ctan (\phi_i-\omega \gamma Vx/c^2 )$$
$$x'=\gamma x$$
Therefore:
$$y-R=x' ctan (\phi_i-\omega V x'/c^2)$$
So, for:
$$\phi_1=0$$
$$y_1-R=x'_1 ctan (-\omega V x'_1/c^2)<0$$
$$\phi_2=\pi$$
$$y_2-R=x'_2 ctan (\pi-\omega V x'_1/c^2)<0$$
I was using $$\phi=0$$ to be parallel to the x-axis at t'=0 to make the equations a little neater.This still doesn't seem right. In the frame of the axle you should have:
$$x'=R cos (\omega t' + \phi)$$
$$y'=R sin (\omega t' + \phi)$$
If this is true, than we can produce scenarios in which reality has two courses which it can take, and no way to determine which course will be taken.
Let's say we do define the top half "invariantly", meaning that the collection of wheel elements constituting the "top half" at some instant in the ground frame is the same as the collection of wheel elements in the top half at some "corresponding" instant in the axle frame. Then the approach you tried in [POST=2848455]post #51[/POST] does become valid (with the correction $$p_{\mathrm{upper}} = - p_{\mathrm{lower}}$$), because it applies to an invariantly defined collection of wheel elements. So setting $$E \equiv E_{\mathrm{upper}} = E_{\mathrm{lower}}$$ and $$p \equiv p_{\mathrm{upper}} = - p_{\mathrm{lower}}$$, you find
$$which are clearly different unless $$p = 0$$ (i.e. a non-rotating wheel).
\begin{align}
E'_{\mathrm{upper}} &= \gamma (E + pv) \,, \\
E'_{\mathrm{lower}} &= \gamma (E - pv) \,.
\end{align}
$$
What do you mean? Isn't that true by definition, since przyk is explicitly talking about the transformed upper elements?Err, no, $$(E,p)'_{upper}$$ isn't the transform of $$(E,p)_{upper}$$.
In any other frame S', moving with speed V wrt S', the energy-momentum transforms according to SR:
$$E'=\gamma(E+pV)$$
Therefore:
$$E'_{upper}=\gamma(E_{upper}+p_{upper}V)$$
What part of [post=2848722]post 60[/post] is relevant?See post 60.
Your parametrization is for spokes that are vertical at $$t'=0, \phi=0, \phi=\pi$$
For those spokes, x'=0 at t=0, making your expression for y'-R undefined.
I was using $$\phi=0$$ to be parallel to the x-axis at t'=0 to make the equations a little neater.
I should probably have kept with your parametrization for consistency, but it quickly simplifies into the expressions I gave anyway.
Also, we should probably decide whether the ground is at y=0 or y=-R, and stick to that convention.
No, Tach, we're quite clear on what is frame dependent.
The set of wheel elements above the fence at any instant is also frame dependent... and that's what we've been talking about ever since the OP.
I note that this is the sum total of Tach's argument on the matter so far:
It "doesn't seem right" to Tach's intuition. Therefore "something is terribly wrong".
Tach, being god-like, apparently isn't required to back up claims with evidence or calculations.
Over 24 hours after I ask Tach to post the derivation he said he'd already done yesterday, and what do I see? Nothing from Tach.
