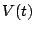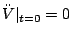Photon Propagation : Straightline or Helix ?

you are-- simply-- not the mathematics mathematician that you believe that you are.
you remind me of the mayans-- they also were not as well with math as they had thought.

 

Log in or Sign up to hide all adverts.

"Pop science" is more often right than not, and certainly more right than most of what you continually claim and tell untruths about [your supposed TOE for example]what I said and as you seem to be at odds with....
"Again, geodesics are straight lines and we were talking about all bodies in curved spacetime including light"
is correct......
http://mathworld.wolfram.com/Geodesic.html
" In the plane, the geodesics are straight lines. On the sphere, the geodesics are great circles (like the equator). The geodesics in a space depend on the Riemannian metric, which affects the notions of distance and acceleration".

You than speak of tidal gravitational forces.........
https://en.wikipedia.org/wiki/Tidal_force
It arises because the gravitational force exerted by one body on another is not constant across it; the nearest side is attracted more strongly than the farthest side. Thus, the tidal force is differential.

At best you seem to be playing with words and pedant, at worst you are just plain wrong. Of course light/photons follow spacetime curvature, that was one of the first verified effects validating GR in the Eddington observations and as evident in many other experiments.
http://www.physicsoftheuniverse.com/topics_relativity_curved.html:

The geometry of Spacetime is altered when mass/energy is present. Light follows that geometry: That has been experimentally verified.

 

Log in or Sign up to hide all adverts.

Since your page was prepared for general audiences, paragraphs two and three give basically the same rubber sheet analogy that Farsight is using. But it's nowhere shown that such an analogy holds for quantitative reasoning even in the limit of low velocities and in the end it is using the phenomena of gravity to "explain" gravity.

In fact, it doesn't quantitatively model Kepler orbits:
http://www.cleyet.org/Someone_is_Wrong/Orbits_on_spandex/GR?.pdf

 

Log in or Sign up to hide all adverts.

.

I can explain in terms anyone can understand (even my grandmother, if I had a living one), why this is flat-out wrong.

If you hold a handful of sand (aka "system of test particles in a ball") and let it fall, it does not maintain its initial shape, but spreads vertically.
This can be explained by a tidal force, and you just 'detected' said force (with a handful of sand).

 

For general audiences yes, and in paragraphs 2 and 3 it says.......
[2] it would appear that light in the presence of gravity follows a curved trajectory, or, put in another way, gravitybends the path of light. In fact, it turns out that gravity is nothing more than curved space, or, more specifically, the curvature or warpage of four-dimensional space-time.
[3] The ants might explain it by saying that the weight is exerting a force of attraction on them, but, from the elevated point of view of the third dimension, it is clear that the ants are merely following the curve of the trampoline and that no actual force is acting on them.
What Farsight said.......
In similar vein when light curves in a gravitational field, it doesn't "follow the curvature of spacetime". Instead it curves because of the spacetime tilt, which is in turn because of the spacetime curvature,
Then in your link it says......
This happy result allows one to analyze the orbits of marbles and coins as they roll across the surface in some detail, providing very nice analogues for a wealth of topics in celestial mechanics, from Kepler's laws to tides and the Roche limit
http://www.cleyet.org/Someone_is_Wrong/Orbits_on_spandex/GR?.pdf

As I said, I still see some "playing with words" from Farsight, and also specifically wrong.
I'm reasonably happy with the link I gave and the conclusion/s.
The rest of that post though you referenced that paragraph from, actually highlights what I saw Farsight being in error about....
The line he objected from me and the one he quoted thus.....
"Again, geodesics are straight lines and we were talking about all bodies in curved spacetime including light"
does need correction though in my opinion....to...
"Again, some geodesics can be straight lines and all straight lines are geodesics, and we were talking about all bodies in curved spacetime including light"
which was corrected anyway in my next link....
http://mathworld.wolfram.com/Geodesic.html
" In the plane, the geodesics are straight lines. On the sphere, the geodesics are great circles"

 

I'm not mangling anything. The "force" of gravity relates to the first derivative, the tidal force relates to the second derivative. The former is in essence the slope, the latter the change in slope - the curvature. Nor am I misteaching anything, so please withdraw your warning. The illustration above gets the point home. A light beam does not curve because "it follows the spacetime curvature".

Not when you don't understand why light curves and end up dismissing Einstein. As I said in this thread, it’s no good using gravity to explain gravity, that’s circular. But the [rubber-sheet] picture isn’t totally wrong. Imagine you’ve placed a whole lot of parallel-mirror light-clocks in an equatorial slice through the Earth and the surrounding space. When you plot all the clock rates, your plot resembles the rubber-sheet picture because clocks go slower when they’re lower. Then the curvature you can see relates to Riemann curvature which relates to curved spacetime. And yes, you measured those clock rates, so yes, it’s a curvature in your metric... How about if I posted a fresh version of that and you tried to explain where it was wrong? You and I both know you won't be able to, and that instead you'll spout platitudes like "cherry picking" or "out of context", and claim that I'm misteaching even though I'm referring to what Einstein said.

 

Huh? Haven't I made this crystal clear already? The "force" of gravity or little g relates to the local gradient in gravitational potential. The slope, as it were. The tidal force relates to spacetime curvature and the way g changes from place to place. If you measure g at the floor to be the same as at the ceiling, there's no detectable tidal force and so no detectable spacetime curvature, but light still curves and your pencil still falls down.

Rubbish. That's nothing to do with the tidal force.

 

Since you are fond of quoting or misquoting Einstein, please show me where he ever said this....Not just any sentence out of context but the full link.
Or alternatively, please show me any reputable link that infers that light/photons do not follow spacetime curvature.
In the meantime.........
http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/grel.html
" Einstein's approach in general relativity is to associate a mass with a curvature of space-time, i.e. the existence of a mass will produce a curvature in space-time around it. From the point of view that light will follow the shortest path, or follows a geodesic of space-time, then if the Sun curves the space around it then light passing the Sun will follow that curvature".
http://pitt.edu/~jdnorton/teaching/HPS_0410/chapters/general_relativity_massive/index.html
"The gravitational deflection of ordinary objects falling in the vicinity of the sun is due to the curvature of the space-time sheets".

Those are just two links that contradict what you so fanatically push both here and elsewhere, and there are hundreds more.
If this "spacetime tilt" that you so often refer to is the 'light cone" analogy, then that's all it is, another analogy, albeit a useful one as analogies can be, although limited in their description.

 

When written out long-hand, the geodesic equations can be written in terms of the metric, the partial derivatives of the metric (with respect to coordinates), the first and second derivatives of the coordinates of the geodesic (in terms of the affine parameter). Since this is sufficient to precisely describe the bending of starlight, the shape and periods of orbits, the advance of the perihelion of Mercury, it would seem that first derivatives of the metric do contain information corresponding to the Newtonian view of gravity as a force. But you can't equate the two, because the metric may have non-zero partial derivatives and still not have anything that Newton would call a force. One simple example has already been given. Another example is:

\(ds^2 = -du^2 \; + \; 2 du \, dv \; + \; 2 a \sin^2 \theta \, dv \, d\phi \; + \; ( v^2 + a^2 \cos^2 \theta) d\theta^2 \; + \; ( v^2 + a^2 ) \sin^2 \theta \, d \phi \)​

So equating "force" with coordinate derivatives of the metric can't be right with the general freedom to choose coordinates granted by Einstein in section one of his 1914 document cited previously. Yet there is a relation, it's just bound up in choice of coordinates so that we can always choose orthonormal Cartesian coordinates where the "force" of gravity vanishes at the space-time origin. These are called free-fall coordinates or a local Lorentz frame.

Tidal force, as we have seen, relates to the Riemann curvature tensor, which is composed from the metric, and its partial derivatives of first and second order. Since the spacetime described by the above metric has Riemann curvature tensor everywhere uniformly zero, it describes Minkowski geometry, which is a solution to the Einstein field equations. So even though the coordinates are peculiar, the spacetime is not curved. On the other hand, if spacetime itself is curved, then we can't make the Riemann curvature tensor go away by choice of coordinates, but there are spacetimes and choices of coordinates where the second derivatives were all zero but the first derivatives were not. Example, if \(g_{\mu\nu}\) is diagonal and has no second derivatives, then

\(R_{0101} = g^{00} ( \partial_{1} g_{00} \partial_{1} g_{00} + \partial_{0} g_{00} \partial_{0} g_{11} ) + g^{11} ( \partial_{0} g_{11} \partial_{0} g_{11} + \partial_{1} g_{00} \partial_{1} g_{11} ) - g^{22} \partial_{2} g_{00} \partial_{2} g_{11} - g^{33} \partial_{3} g_{00} \partial_{3} g_{11} \)​

which need not be zero. So second-order effects like tidal forces are not solely associated with second derivatives.

What then should we make of your claim that "slope" is responsible for first-order gravitational effects? Such a claim is either based on a particular and parochial choice of a coordinate system, in which case you have the burden to show you have not conflated coordinate choice effects with physics, or you have a coordinate-free way to describe how the space-time metric changes with position. Einstein introduces the Christoffel symbols from late 19th century mathematics to build a type of derivative on manifolds that doesn't include effects from choice of coordinates. But unfortunately for your position, \(\nabla_{\alpha} g_{\beta\gamma} = 0\), so there is no "slope" of the metric in evidence. Similar statements hold in more modern mathematics of GR. These same Christoffel symbols are used to describe geodesics which remain unchanged under change of coordinates. And geodesics are the topic of this thread.

So obviously, if there is no coordinate-free way to get a non-zero "slope" from the metric, then there can be no non-zero second derivative. So what is the Riemman curvature tensor in coordinate-free language? It is the commutator of the second coordinate-free derivative of smooth vector fields.

\(R_{\beta\gamma\delta}^{\alpha} u^{\beta} v^{\gamma} w^{\delta} = v^{\gamma} w^{\delta} \left( \nabla_{\gamma} \nabla_{\delta} u^{\beta} - \nabla_{\delta} \nabla_{\gamma} u^{\beta} \right) \).​

In "slope" you have proposed an unworkable scheme and one that seems based on mere analogy with the rubber sheet model.

I would disagree, but PMs are the required format for discussion individual moderator actions.

The illustration is not to scale, labeled, or derived from theoretical principle. Also, physics is not about "because" principles but about the behavior of observable phenomena; physics cannot distinguish two "because" reasons that lead to predictions of the same behavior. But since the geodesic principle applies both to massive particles and light, I choose it for parsimony. Also, 100 years of GR including Einstein's 1914 paper. Moreover, you have not distinguished your particular views from the shape of a null geodesic. The only way you can support your view is by calculating both, showing all your assumptions and approximations, finding a difference between the two and finding that physical observation confirms you view over mine. The only way you can support your view is physics is by showing it is better physics.

Calculation and unification go a long way towards demonstrating I have a good understanding of the behavior of light in a gravitational field and since my textbook doesn't contradict Einstein (except for his typos, which were many) I don't think the thousands of students of GR like myself have dismissed Einstein. This post and your warnings, are about your behavior, not Einstein's.

So you don't care if the rubber sheet model fails to reproduce the dynamics of even Newtonian gravity, you like it because it has axial symmetry and has increasing slope nearer the center which makes it vaguely resembles the Newtonian potential and a plot of clock rates at fixed spatial coordinates in the Schwarzschild coordinates and the related, but not identical, embedding diagram. But the only way you know this is by graphing the Newtonian potential or making GR calculations from first principles. So it's a cartoon like your picture of light bending. It explains nothing because it is wrong in principle and the details. Further, the rubber sheet requires the phenomenon of gravity to work in the first place.

Do you mean the visible curvature of the 2-D surface of the rubber sheet has its own Riemann curvature which you can compare and contrast with the Riemann curvature of 4-dimensional space-time? You certainly can't equate them. You might even introduce the concept of Gaussian curvature. But that's only useful as a toy prerequisite in teaching preliminaries to GR. If that was enough, wouldn't Einstein have stopped there rather than to master tensor calculus on curved manifolds?

Even if you built a toy that gave exactly the right trajectories in the limit of low velocities, had exactly the right profile as your plot of clock rates or was an exactly physical model of the embedding diagram, such a toy would be based on the Schwarzschild geometry, and there is more to GR than the Schwarzschild geometry.

In addition to confusing "spacetime curvature," a property of spacetime, with "curved spacetime", spacetime with a non-zero value of that property, I believe you are misusing "platitudes". Just because being warned by moderation and given specific instances of where you take tiny quotes out of context doesn't provoke thought in you doesn't mean they were done without deliberation and causing others to think about them.

 

http://math.ucr.edu/home/baez/einstein/node5.html

 

That's a handful of sand in freefall with a time scale which is long relative to the scale of spacetime curvature.
So since most of the posters here are terrestrial, that's a handful of very expensive sand (since it needs to be in orbit).

 

I don't follow. Are you saying Baez' example isn't relevant because of the short time scale?

 

Baez is correct but you didn't calculate how much distortion per time. So it's not something you would notice in the short time your handful of sand would take to fall to the floor.

 

Here you go, see the Einstein digital papers, where Einstein said light curves because the speed of light is spatially variable. Now it's your turn. You give me a link that has Einstein saying light follows spacetime curvature. You won't be able to, because he never ever did.

I like hyperphysics, and I think Rod nave is a saint. But I have to say this paragraph is rather garbled and misleading. I'll explain it step by step:

Einstein's approach in general relativity is to associate a mass with a curvature of space-time

That's fairly reasonable. We might say energy rather than mass, or refer to a metric, but I don't think anybody would have any serious objection to the above.

, i.e. the existence of a mass will produce a curvature in space-time around it.

This is slightly flawed in that the "around it" is starting to confuse space and spacetime, but OK, no serious objection.

From the point of view that light will follow the shortest path, or follows a geodesic of space-time

This is starting to go wrong, in that light curves. It doesn't follow the shortest path. Its path is described by a geodesic, but it doesn't follow that geodesic, just as you don't follow your world line.

then if the Sun curves the space around it then light passing the Sun will follow that curvature.

Wrong on two counts. The Sun doesn't curve the space around it, see Baez: "Similarly, in general relativity gravity is not really a 'force', but just a manifestation of the curvature of spacetime. Note: not the curvature of space, but of spacetime. The distinction is crucial". Curved spacetime is not curved space plus curved time. It's a curvature in your plot of measurements of space and time, or a curvature in your metric, metric being to do with measurement. And light definitely doesn't follow this spacetime curvature, as per my illustration of the plastic sheet:

Please Register or Log in to view the hidden image!

This is OK. Look at the picture above. If the sheet wasn't curved, the right-hand portion of it wouldn't have a gradient. But make no mistake, light curves because of the gravitational gradient which is related to what's nowadays known as the "coordinate" speed of light. It curves even where there's no detectable change in the gravitational gradient. In similar vein if you tilt a rigid board and roll a marble across it, the path of the marble is curved even though the board isn't. It doesn't follow the curvature of the board.

I'm not fanatically pushing anything. I'm merely correcting the cargo-cult popscience you've been peddling. By referring to Einstein and explaining GR in simple terms that you can understand. What's not to like?

 

Perhaps a high speed camera? Baez talks about how the shape of a ball of particles changes as it free falls, in a manner suggesting it can be seen.

 

How would you explain the difference in apparent position of stars near the sun during a total eclipse? The accepted wisdom is: gravitational lensing, or curvature of the space around the sun.

All the observations of gravitational lensing are observations of the curving of space and of light following curved geodesics.

 

I've seen you reference that before: Perhaps Einstein may have been lazy in his writings, plus the fact that he was obviously addressing other professionals.
Simply put light has further to travel in curved spacetime and I'm sure Einstein was aware of that.
Einstein also wrote those 100 years ago, and much progress has been made since. No, I'm not going to find where Einstein said any differently, other than again to say "The speed of light does not change" and that simple fact aligns with all experimental results that have been done since Einstein said that 100 years ago.
http://www.speed-light.info/speed_of_light_variable.htm
However in the presence of gravity if I am at a different location than yours then I could measure the speed of light at your location to be any value smaller than or greater than 299792.458 km/sec. It depends on where I am and where you are (it depends on locations). So in the presence of gravity the speed of light becomes relative (variable depending on the reference frame of the observer). This does not mean that photons accelerate or decelerate; this is just gravity causing clocks to run slower and rulers to shrink.

Garbled? Nonsense! It is evidenced by many experiments including GP-B.

So in effect you are "correcting" the accepted mainstream interpretation of how GR is viewed today and how it has been overwhelmingly evidenced.
The great man you so often quote was also a humble human being, and admitted when in error. You most certainly are fanatically pushing your nonsense and treating Einstein with contempt in doing it.
Anyone one claims he has a TOE needs to be treated with a grain of salt in all respects.
Also while you may be technically in advance of me on certain issues re SR/GR, others here have certainly mathematically revealed your nonsense and of course if you were correct, we would see you lined up for the Physics Noble in November.
[Instead of fading into oblivion]

 

I don't, instead I take note of Newton's opposition to action-at-a-distance and his talk of light curving. See his letter to Richard Bentley : "That gravity should be innate inherent & {essential} to matter so that one body may act upon another at a distance through a vacuum without the mediation of any thing else by & through which their action or force {may} be conveyed from one to another is to me so great an absurdity that I beleive no man who has in philosophical matters any competent faculty of thinking can ever fall into it". Also see Opticks query 20: "Doth not this aethereal medium in passing out of water, glass, crystal, and other compact and dense bodies in empty spaces, grow denser and denser by degrees, and by that means refract the rays of light not in a point, but by bending them gradually in curve lines?" It's not totally unlike Einstein's description, particularly when you note Einstein's 1920 Leyden Address where he referred to space as the aether of general relativity.

The force of gravity "vanishes" when you're falling in that when you drop your pencil it appears to hover in front of your face. This was the essence of Einstein's happiest thought. But let's not forget that you are falling, and that unless you have a parachute, you will shortly be reminded that the "force" of gravity has not truly vanished.

Agreed. See section 20 of Relativity: the Special and General Theory where Einstein said this: “We might also think that, regardless of the kind of gravitational field which may be present, we could always choose another reference-body such that no gravitational field exists with reference to it. This is by no means true for all gravitational fields, but only for those of quite special form. It is, for instance, impossible to choose a body of reference such that, as judged from it, the gravitational field of the earth (in its entirety) vanishes”.

You know full well that we talk of the first and second derivatives of potential.

It's not an unworkable and you know it. The gradient or slope or tilt features extensively in gravity and GR, see the Einstein digital papers, and note the tilted lightcones from this Stanford article:

Please Register or Log in to view the hidden image!

If you've got anything to say to me, you can say it in public.

Referring to the Einstein digital papers.

Not so. I support my view by showing that it's Einstein's view, and that you can only support your view by dismissing Einstein.

No, it's about physics, and those warnings are undeserved because I'm right, because Einstein's right. Withdraw them.

I didn't say that. Don't put words in my mouth.

I didn't invent it, but I did explain how it can be justified.

I haven't confused anything, nor am I misusing anything, and I'm not quoting Einstein out of context either. You however are dismissing Einstein because what the guy said doesn't tally with your own misunderstanding of general relativity. I recommend you read the Einstein digital papers, then revisit your text book, whereupon you will appreciate that in some respects, that textbook, which you've been treating like a bible, is wrong.

 

That's wrong. Rpenner will confirm this.

Again, wrong. What happens is that a concentration of energy in the guise of a massive star "conditions" the surrounding space, altering its metrical or measurement properties, this effect diminishing with distance in a non-linear or curved fashion. The result is a gravitational field, which is modelled as curved spacetime. Ask rpenner for an alternative wording.

 

It "conditions" the surrounding space by curving it, so you see a lensing effect which can be compared to an optical lens which also bends light.

Space is part of spacetime. An image of gravitational lensing from the Hubble 'scope doesn't show any "time curvature", the effect is purely spatial; space is bent by gravity.