Movement of electrons in atomic orbitals

[Muzaffar]

Thank you so much exchemist once again for doing your best. I've probably got a layout of the concept of particles as waves (thanks to your "light" example) but for now i think its better if i remember the basic concept of orbitals as "a region with a high probability of finding a an electron". Ill probably be studying QM sometime as well. I'm sure ill have a better idea of waves then. Ill be sure to look back to this essential thread as well. Thanks a lot

That is a question that is still argued over, among those interested in the philosophy of Quantum Theory. You get this with light of course. We can see light reflected, refracted and diffracted, and we know it has a wavelength and frequency, all of which are wave properties. But it seems it can only be emitted or absorbed in discrete units (which we call photons) and it can exert pressure on a surface on which it falls, which is particle-like behaviour. With beams of electrons and other particles of matter, we find we can also get diffraction effects (interference fringes for example). Which is wavelike behaviour! The wavelength of a particle is related to its momentum, by de Broglie's relation: lambda = h/p, in which lambda = wavelength, p = momentum and h is Planck's constant. So higher momentum particles have a shorter wavelength - or higher frequency.

As to what the "waves" are, that's a good question. The things that make a thing seem to exist are the properties of it that one can measure. With Quantum Mechanics one needs a short excursion into the maths and then back again to see how physical properties relate to the waves. In QM, all the information about a wave-particle in a particular state is contained in something called its "state function" or eigenfunction, or sometimes wavefunction. This complex-form mathematical function has wave-like qualities. (If you ever study alternating current theory in physics, you will find complex numbers crop up there as well - because that is also a theory of waves.) To determine the value of a physical property, such as energy or momentum, one "operates" mathematically on the state function with the appropriate QM operator. The simplest operation is for position. To find the probability of the particle being found in a given volume of space, one multiplies the function by its complex conjugate (this is the complex number equivalent of squaring it) and integrates this over the volume of space in question.

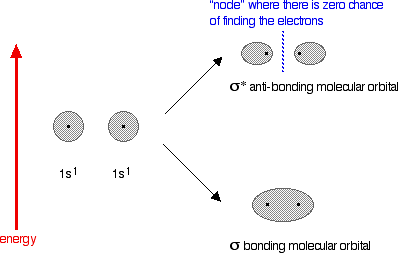
So, you can think of the "waves" as being waves of probability, or rather, the square root of probability. The pictures you see in textbooks of the shapes of orbitals are plots of the probability obtained in this way. But you cannot hope to know everything about a particle at once, in the way you can in classical physics. Heisenberg's Uncertainty Principle says that delta p.delta x >/=h/4 pi, in which delta p and delta x are the uncertainty about the momentum and position of the particle and h is again Planck's Constant. This is why you cannot track the "orbit" of an electron. If you could write down an orbit for it, you would be able to say what its position and momentum were exactly. In QM, this CANNOT be done. And the reason why is the inherently fuzzy nature of the probability waves which determine what you are allowed to know about a system of particles.

It is not easy and has troubled the best minds of science. Einstein himself hated it, saying God does not play dice. But, all the evidence is that God DOES play dice and that probability waves are how matter really does behave on the atomic scale.

My best advice to you, since you are starting out on this mysterious adventure, is to pay close attention to anything you are taught in physics concerning waves: wavelength and frequency, phase, amplitude and energy, reflection, refraction, diffraction, resonance and standing waves, constructive and destructive interference and what happens when you superimpose waves of different frequencies on top of one another. All these come up time after time in QM and are used to explain all sort of things in chemistry, from atomic and molecular spectra to chemical bonding itself. So if you understand waves, you will "get" QM - at least qualitatively.

 

[exchemist]

Thank you so much exchemist once again for doing your best. I've probably got a layout of the concept of particles as waves (thanks to your "light" example) but for now i think its better if i remember the basic concept of orbitals as "a region with a high probability of finding a an electron". Ill probably be studying QM sometime as well. I'm sure ill have a better idea of waves then. Ill be sure to look back to this essential thread as well. Thanks a lot

OK, good luck, and have fun.

 

[Layman]

It has advanced, substantially. We now have Frontier Molecular Orbital Theory which correctly predicts some of the oddities in chemistry (things like why rule violations occur).

I think that even these types of orbitals have been shown to be at distances where the circumference of these orbitals are distances where the wavelength of the electron will be a full wave length. It was presented together in my chemistry course.

There is a zero probability of the electron being at distances that are not a full wave length, so then they are restricted to these orbitals that don't have a width. That is why I think the electron must move around the atom, in order for it to have this type of self interaction. There could only be one electron in a orbital at a time.

Then when the electron changes from one orbital to another it vanishes and is not detectable. So then it as if the electron can in effect cancel itself out since the circumference of the orbital will be a half wave length. It then emits a photon to change its energy level to be appropriate for it be in a lower orbital, or it can absorb photon to be in a higher orbital. Then the electron makes a quantum leap to the other orbital, in effect jumping over the half wave lengths of circumference.

I find it hard to imagine how this could all take place if the electron wasn't at least traveling at "luminal" speeds around the atom. For instance, you couldn't have a lazy river in a theme park that makes waves that lengths are shorter than the circumference of the river and then have no waves with the wave machine still turned on just because the lazy river was a half wave length in circumference. There would always be waves in the river that would not be able to catch up to the other waves in the river. Then if they did get around to canceling all the waves in the river with the wave machine still on, it would then create waves.

There would have to be some sort of superluminal communication between the waves of electrons in the atom.

 

[exchemist]

I think that even these types of orbitals have been shown to be at distances where the circumference of these orbitals are distances where the wavelength of the electron will be a full wave length. It was presented together in my chemistry course.

There is a zero probability of the electron being at distances that are not a full wave length, so then they are restricted to these orbitals that don't have a width. That is why I think the electron must move around the atom, in order for it to have this type of self interaction. There could only be one electron in a orbital at a time.

Then when the electron changes from one orbital to another it vanishes and is not detectable. So then it as if the electron can in effect cancel itself out since the circumference of the orbital will be a half wave length. It then emits a photon to change its energy level to be appropriate for it be in a lower orbital, or it can absorb photon to be in a higher orbital. Then the electron makes a quantum leap to the other orbital, in effect jumping over the half wave lengths of circumference.

I find it hard to imagine how this could all take place if the electron wasn't at least traveling at "luminal" speeds around the atom. For instance, you couldn't have a lazy river in a theme park that makes waves that lengths are shorter than the circumference of the river and then have no waves with the wave machine still turned on just because the lazy river was a half wave length in circumference. There would always be waves in the river that would not be able to catch up to the other waves in the river. Then if they did get around to canceling all the waves in the river with the wave machine still on, it would then create waves.

There would have to be some sort of superluminal communication between the waves of electrons in the atom.

Well, like anyone, you are free to speculate, but little of what you say here bears much resemblance to the current QM model of electrons in an atom or molecule.

To take one instance, electronic transitions between orbitals do not involve any "vanishing". The electron eigenfunction couples to the oscillating field of the photon being absorbed or emitted and the transition takes a finite time to occur, described throughout the process by the time-dependent form of the Schroedinger equation (as opposed to the time-independent one, which describes stable states).

 

[Layman]

Well, like anyone, you are free to speculate, but little of what you say here bears much resemblance to the current QM model of electrons in an atom or molecule.

If you take a look at the wiki on Superluminal Communication you will find that one theory or experiment that shows this is Evanescent Wave Coupling . I think the electron wave in the orbitals of the atom would be a form of Evanescent Wave Coupling .

To take one instance, electronic transitions between orbitals do not involve any "vanishing".

I don't agree, this theory is based off of spectral lines.

As you can see there are gaps in the spectral lines so that the orbitals where there are not electrons they do not create spectral lines. It is as though the electron does not exist at these ranges where it could then create spectral lines in the gaps between the lines that it does actually create. The theory behind what causes these spectral lines has changed but the fact remains that spectral lines still do occur and is what is seen from experiment.

The electron eigenfunction couples to the oscillating field of the photon being absorbed or emitted and the transition takes a finite time to occur, described throughout the process by the time-dependent form of the Schroedinger equation (as opposed to the time-independent one, which describes stable states).

This is also the same equation that has been attributed to leading to alternate universes. But then the "universes" where electrons could exist between different orbitals don't ever exist, this is why I often preferred the Copenhagen Interpretation . The electron can never be found between orbitals via any type of experiment, ever. If the Schrodinger Equation says that there should be electrons between orbitals then it would seem like it would be incomplete. It would be accounting for things that are happening that actually never do. We haven't ever seen decoherence from a universe that has spectral lines to a "universe" where there was not spectral lines. It is a consistent result of experiment.

 

[exchemist]

spectral lines[/url].

As you can see there are gaps in the spectral lines so that the orbitals where there are not electrons they do not create spectral lines. It is as though the electron does not exist at these ranges where it could then create spectral lines in the gaps between the lines that it does actually create. The theory behind what causes these spectral lines has changed but the fact remains that spectral lines still do occur and is what is seen from experiment.

.

No, the gaps in the spectrum are simply because the electron can only occupy certain energy levels and it is transitions between these that create spectral lines. These transitions therefore involve energy changes only at a discrete and limited set of energy values. Since the frequency of the photons emitted or absorbed in this process depend on their energy, you get only a discrete number of spectral lines from this process. The gaps are at all the energies that do not correspond to these transitions. Nothing whatever to do with electrons "vanishing".

 

[Aqueous Id]

Correct. Layman has taken the Balmer emission series for Hydrogen and jumped to conclusions about how to interpret it. He mentions encountering this in a chemistry class, but forgot the Rydberg equation (spectral line wavelength is related to the change in energy of the electron as it traverses orbitals). It would of course be problematic to assign spectral lines to electrons (or orbitals) since you would be assigning too many electrons to the atom. In this case, his assumption implies that Hydrogen has 4 electrons, and it gets worse if you include the other series not mentioned. He also said the theory has changed but this isn't quite correct. Balmer in 1885 had no way of knowing his discovery was a subset of the ways energy transitions can be induced as per Rydberg's later more general formulation. From a very early perspective, then we can see that the theory of quantum state of the electron, as a function in change of principal quantum number, as further related to the difference in mean radii of two two orbitals in question, has not changed, at least not as far as how spectrum line wavelength applies to the electron state changes. The other thing missing from this picture is that spectra are collected on bulk matter, obviously not on individual atoms, so the displayed result shows all the permutations for all the atoms in the sample under test, for which electron transitions are randomly distributed events.

 

[arauca]

Correct. Layman has taken the Balmer emission series for Hydrogen and jumped to conclusions about how to interpret it. He mentions encountering this in a chemistry class, but forgot the Rydberg equation (spectral line wavelength is related to the change in energy of the electron as it traverses orbitals). It would of course be problematic to assign spectral lines to electrons (or orbitals) since you would be assigning too many electrons to the atom. In this case, his assumption implies that Hydrogen has 4 electrons, and it gets worse if you include the other series not mentioned. He also said the theory has changed but this isn't quite correct. Balmer in 1885 had no way of knowing his discovery was a subset of the ways energy transitions can be induced as per Rydberg's later more general formulation. From a very early perspective, then we can see that the theory of quantum state of the electron, as a function in change of principal quantum number, as further related to the difference in mean radii of two two orbitals in question, has not changed, at least not as far as how spectrum line wavelength applies to the electron state changes. The other thing missing from this picture is that spectra are collected on bulk matter, obviously not on individual atoms, so the displayed result shows all the permutations for all the atoms in the sample under test, for which electron transitions are randomly distributed events.

Does QM. have any explanation for a benzene ring or even an acetylene molecule ?

 

[exchemist]

Does QM. have any explanation for a benzene ring or even an acetylene molecule ?

Certainly. For example the explanation of "resonance", and even more so of aromaticity, in conjugated rings depends on it.

 

[Trippy]

Does QM. have any explanation for a benzene ring or even an acetylene molecule ?

Yes. Molecular orbital theory not only provides a good explanation for it, but for the chemistry of benzene.

 

[arauca]

Certainly. For example the explanation of "resonance", and even more so of aromaticity, in conjugated rings depends on it.

Can you give some detail explanation.

 

[Trippy]

Can you give some detail explanation.

Molecular orbitals are predicted by quantum mechanics. It's a consequence of the delocalization of electrons.

In the simplest case, that of Hydrogen.

You start off with two spheres, the 1S orbital, and bring them together. Quantum mechanics predicts that the wave functions of the two 1s orbitals add to give two wave functions. The first wave function is the result of adding two 1s orbitals together with the same phase, is a bonding orbital because it concentrates electron density between the hydrogen atoms, and stabilizes the molecule. The second wave function is the result of adding to 1s orbitals of opposing phases, is an antibonding orbital because it concentrates electron density away from the center and destabilizes the molecule. The Pauli exclusion principle predicts that only two electrons can occupy an orbital, however, bringing two hydrogen atoms together only gives you a total of two electrons, so they can both occupy the same orbital. Quantum mechanics predicts that the bonding orbital is lower energy than the antibonding orbital, both electrons occupy this orbital, and so dihydrogen is stable at STP. The bonding orbital is the highest occupied molecular orbital (HOMO) and the antibonding orbital is the lowest unoccupied molecular orbital (LUMO).

Chemistry occurs when another molecule or atom comes along and starts contributing electron density to the lowest unoccupied molecular orbital of another molecule. In the case of hydrogen, this splits the molecule.

The same basic principles apply to Benzene, only the result is a little more complicated because there are more atoms involved, and you're using p-orbitals:

Resonance occurs because there are molecular orbitals that delocalize electrons across the whole molecule. This approach also explains the rules regarding aromaticity at the same time that it explains the paramagnetism and reactivity of oxygen:

 

[exchemist]

Molecular orbitals are predicted by quantum mechanics. It's a consequence of the delocalization of electrons.

In the simplest case, that of Hydrogen.

You start off with two spheres, the 1S orbital, and bring them together. Quantum mechanics predicts that the wave functions of the two 1s orbitals add to give two wave functions. The first wave function is the result of adding two 1s orbitals together with the same phase, is a bonding orbital because it concentrates electron density between the hydrogen atoms, and stabilizes the molecule. The second wave function is the result of adding to 1s orbitals of opposing phases, is an antibonding orbital because it concentrates electron density away from the center and destabilizes the molecule. The Pauli exclusion principle predicts that only two electrons can occupy an orbital, however, bringing two hydrogen atoms together only gives you a total of two electrons, so they can both occupy the same orbital. Quantum mechanics predicts that the bonding orbital is lower energy than the antibonding orbital, both electrons occupy this orbital, and so dihydrogen is stable at STP. The bonding orbital is the highest occupied molecular orbital (HOMO) and the antibonding orbital is the lowest unoccupied molecular orbital (LUMO).

Chemistry occurs when another molecule or atom comes along and starts contributing electron density to the lowest unoccupied molecular orbital of another molecule. In the case of hydrogen, this splits the molecule.

The same basic principles apply to Benzene, only the result is a little more complicated because there are more atoms involved, and you're using p-orbitals:

Resonance occurs because there are molecular orbitals that delocalize electrons across the whole molecule. This approach also explains the rules regarding aromaticity at the same time that it explains the paramagnetism and reactivity of oxygen:

Very nice!

 

[arauca]

Thanks but this nothing new for me , I am familiar with sigma bonds and pi bonds which are the double bonds . but the triple bond is a little less understood because some how in acetylene the pi bond is overcrowded

 

[Trippy]

Thanks but this nothing new for me , I am familiar with sigma bonds and pi bonds which are the double bonds . but the triple bond is a little less understood because some how in acetylene the pi bond is overcrowded

Not a smuch as you might think.

 

[Trippy]

Although I suppose, arguably, the flipside is that the 'overcrowding' you refer to is part of what makes acetylene so unstable (explosively so under the right conditions).

 

[Layman]

Correct. Layman has taken the Balmer emission series for Hydrogen and jumped to conclusions about how to interpret it. He mentions encountering this in a chemistry class, but forgot the Rydberg equation (spectral line wavelength is related to the change in energy of the electron as it traverses orbitals). It would of course be problematic to assign spectral lines to electrons (or orbitals) since you would be assigning too many electrons to the atom. In this case, his assumption implies that Hydrogen has 4 electrons, and it gets worse if you include the other series not mentioned. He also said the theory has changed but this isn't quite correct. Balmer in 1885 had no way of knowing his discovery was a subset of the ways energy transitions can be induced as per Rydberg's later more general formulation. From a very early perspective, then we can see that the theory of quantum state of the electron, as a function in change of principal quantum number, as further related to the difference in mean radii of two two orbitals in question, has not changed, at least not as far as how spectrum line wavelength applies to the electron state changes. The other thing missing from this picture is that spectra are collected on bulk matter, obviously not on individual atoms, so the displayed result shows all the permutations for all the atoms in the sample under test, for which electron transitions are randomly distributed events.

Well since you go around all the time wearing a pointed hat maybe you would like to take a look at the wiki for what you mention the Balmer Series and the Borh Model that according you hasn't changed since it was based off of spectral lines.

"In the simplified Rutherford Bohr model of the hydrogen atom, the Balmer lines result from an electron jump between the second energy level closest to the nucleus, and those levels more distant. Shown here is a photon emission. The transition depicted here produces H-alpha, the first line of the Balmer series. For hydrogen () this transition results in a photon of wavelength 656 nm (red)."

 

[Layman]

No, the gaps in the spectrum are simply because the electron can only occupy certain energy levels and it is transitions between these that create spectral lines. These transitions therefore involve energy changes only at a discrete and limited set of energy values. Since the frequency of the photons emitted or absorbed in this process depend on their energy, you get only a discrete number of spectral lines from this process. The gaps are at all the energies that do not correspond to these transitions. Nothing whatever to do with electrons "vanishing".

So then you don't even believe that an electron quantum leaps in the atom from one orbital to another?

 

[Read-Only]

So then you don't even believe that an electron quantum leaps in the atom from one orbital to another?

No, that's not what he said or even implied. He clearly said, in bold even, only at a discrete and limited set of energy values. That means that there are no intermediate "locations." It's like either A or B - there's no place in between for electrons.

 

[exchemist]

So then you don't even believe that an electron quantum leaps in the atom from one orbital to another?

Sure it does. Just not in some magical "instantaneous" process involving vanishing and reappearance. It's very rapid but it is not instantaneous. It's a coupling "resonance" between the initial and final states and with the oscillating electric field (usually) of the photon.

Re your other post, in the Bohr model, yes, you would need to have magical instantaneous disappearance and reappearance, as classical mechanics can't explain the jumps. BUT the Bohr model predates the QM model and is now of historical interest only. By the way the classical Bohr model can't explain how you can have an electron in an s orbital either. Electrons in s orbitals have zero angular momentum, and yet do not fall into the nucleus - although they can go right up to it, unlike electrons in orbitals that do have angular momentum, such as p, d and f.