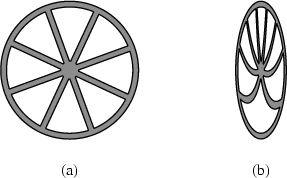
Here's another thought experiment in SR...
We have a spaceship called S1 moving past another spaceship called S2.
S1 is 10 miles long in its rest frame and is moving at .8c relative to S2.
Inside S1 we have a 10 inch diameter bicycle tire rolling along the ground.
Now then, from the reference frame of S2, the length of S1 = $$10*\sqrt{1-.8^2}$$= 6 miles long.
From the reference frame of S2, the bicycle tire inside S1 is length contracted into an ellipse.
The equation of this ellipse if plotted on xy-coordinates would be $$\frac{25x^2}{9}+y^2=25$$
What is the length of the perimeter of this contracted bicycle tire (ellipse)?
Well, $$\frac{\mathrm{d} }{\mathrm{d} x} = \frac{-5x}{3\sqrt{9-x^2}}$$
Arc Length = $$\int_{0}^{3}\sqrt{1+\frac{25x^2}{81-9x^2}}dx = 6.38174971583125$$
This is 1/4 of the perimeter, so the perimeter is 25.526998863325 inches.
Now let's divide the rest length of the ground by the rest length of the perimeter and the contracted length of the ground by the contracted length of the perimeter.
$$\frac{10}{10\pi}=0.3183098862$$
$$\frac{6}{25.526998863325}= 0.235045256676$$
Now, notice that these two numbers are not the same! Why does this spell trouble?
It spells trouble because if we imagine an ink spot on the bicycle tire, it will leave a different number of spots on the ground according to the different reference frames.
According to S1, $$\frac{5280*12*10}{10\pi} = 20,168$$ ink spots are left on the ground.
According to S2, $$\frac{5280*12*6}{25.5269988633236} = 14,892$$ ink spots are left on the ground.
So, we are immediately faced with a paradox.
We have a spaceship called S1 moving past another spaceship called S2.
S1 is 10 miles long in its rest frame and is moving at .8c relative to S2.
Inside S1 we have a 10 inch diameter bicycle tire rolling along the ground.
Now then, from the reference frame of S2, the length of S1 = $$10*\sqrt{1-.8^2}$$= 6 miles long.
From the reference frame of S2, the bicycle tire inside S1 is length contracted into an ellipse.
The equation of this ellipse if plotted on xy-coordinates would be $$\frac{25x^2}{9}+y^2=25$$
What is the length of the perimeter of this contracted bicycle tire (ellipse)?
Well, $$\frac{\mathrm{d} }{\mathrm{d} x} = \frac{-5x}{3\sqrt{9-x^2}}$$
Arc Length = $$\int_{0}^{3}\sqrt{1+\frac{25x^2}{81-9x^2}}dx = 6.38174971583125$$
This is 1/4 of the perimeter, so the perimeter is 25.526998863325 inches.
Now let's divide the rest length of the ground by the rest length of the perimeter and the contracted length of the ground by the contracted length of the perimeter.
$$\frac{10}{10\pi}=0.3183098862$$
$$\frac{6}{25.526998863325}= 0.235045256676$$
Now, notice that these two numbers are not the same! Why does this spell trouble?
It spells trouble because if we imagine an ink spot on the bicycle tire, it will leave a different number of spots on the ground according to the different reference frames.
According to S1, $$\frac{5280*12*10}{10\pi} = 20,168$$ ink spots are left on the ground.
According to S2, $$\frac{5280*12*6}{25.5269988633236} = 14,892$$ ink spots are left on the ground.
So, we are immediately faced with a paradox.
Last edited: