Length contraction problem.

[Zeno]

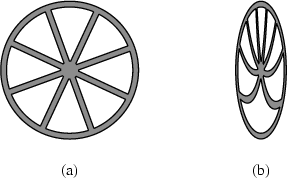
Here's another thought experiment in SR...
We have a spaceship called S1 moving past another spaceship called S2.
S1 is 10 miles long in its rest frame and is moving at .8c relative to S2.
Inside S1 we have a 10 inch diameter bicycle tire rolling along the ground.
Now then, from the reference frame of S2, the length of S1 = $$10*\sqrt{1-.8^2}$$= 6 miles long.
From the reference frame of S2, the bicycle tire inside S1 is length contracted into an ellipse.
The equation of this ellipse if plotted on xy-coordinates would be $$\frac{25x^2}{9}+y^2=25$$
What is the length of the perimeter of this contracted bicycle tire (ellipse)?

Well, $$\frac{\mathrm{d} }{\mathrm{d} x} = \frac{-5x}{3\sqrt{9-x^2}}$$

Arc Length = $$\int_{0}^{3}\sqrt{1+\frac{25x^2}{81-9x^2}}dx = 6.38174971583125$$
This is 1/4 of the perimeter, so the perimeter is 25.526998863325 inches.
Now let's divide the rest length of the ground by the rest length of the perimeter and the contracted length of the ground by the contracted length of the perimeter.
$$\frac{10}{10\pi}=0.3183098862$$
$$\frac{6}{25.526998863325}= 0.235045256676$$

Now, notice that these two numbers are not the same! Why does this spell trouble?
It spells trouble because if we imagine an ink spot on the bicycle tire, it will leave a different number of spots on the ground according to the different reference frames.
According to S1, $$\frac{5280*12*10}{10\pi} = 20,168$$ ink spots are left on the ground.
According to S2, $$\frac{5280*12*6}{25.5269988633236} = 14,892$$ ink spots are left on the ground.
So, we are immediately faced with a paradox.

 

[Pete]

Firstly, I don't think your ellipse circumference is quite right, but that doesn't matter, because there's a larger problem.

Now let's divide the rest length of the ground by the rest length of the perimeter and the contracted length of the ground by the contracted length of the perimeter.

It doesn't work that way.

In the rest frame of the ground, different parts of the perimeter are aligned in different directions, and so contracted by different amounts.
This means that the ellipse perimeter does not give the distance traveled in one turn of the wheel.

 

[Tach]

Firstly, I don't think your ellipse circumference is quite right, but that doesn't matter, because there's a larger problem.

Indeed, his ellipse equation is incorrect, the correct equation is:

$$(\frac{x}{\gamma(v)}-vt)^2+y^2=r^2$$

where v is the speed of the center of the wheel and r is the radius of the circle.

It doesn't work that way.

In the rest frame of the ground, different parts of the perimeter are aligned in different directions, and so contracted by different amounts.
This means that the ellipse perimeter does not give the distance traveled in one turn of the wheel.

Correct again, for a proper description, see here

 

[Pete]

Indeed, his ellipse equation is incorrect, the correct equation is:

$$(\frac{x}{\gamma(v)}-vt)^2+y^2=r^2$$

where v is the speed of the center of the wheel and r is the radius of the circle.

No, his ellipse equation is fine, it's an ellipse with major axis 10, semimajor axis 6. (r=5, gamma=.6)
Granted he's only given the instantaneous equation at t=0, but that's sufficient for calculating the circumference.

It's the circumference calculation that isn't quite right.

Correct again, for a proper description, see here

Well, that link is actually about a different problem, in which a wheel is rolling at relativistic speed relative to the surface. And it is describing how light scattering off the rolling wheel is perceived by a naive observer or video camera.

Zeno's posted problem is about a wheel rolling slowly relative to the surface, but considering a reference frame in which the surface is moving relativistically. And we're not concerned with the perceptual artefacts.

 

[Tach]

No, his ellipse equation is fine, it's an ellipse with major axis 10, semimajor axis 6. (r=5, gamma=.6)
Granted he's only given the instantaneous equation at t=0, but that's sufficient for calculating the circumference.

It is a little more complicated than that, see here.

Well, that link is actually about a different problem, in which a wheel is rolling at relativistic speed relative to the surface. And it is describing how light scattering off the rolling wheel is perceived by a naive observer or video camera.

True but , among all these things, the website gives the correct formalism of the rolling circle against the straight line trajectory. Ignore the raytracing part, if you look at the animations (pick the first one) it shows how the markers on the wheel line up with the markers on the ground). If the wheel rolls without slippage in $$S_1$$ there is no guarantee that the ellipse rotates without slippage from the pespective of $$S_2$$, you need to calculate the exact motion. If the circle fits $$\frac{10}{10 \pi}$$ into the length of $$S_1$$ as Zeno claims, you need to calculate how many times it fits from the perspective of $$S_2$$. But the motion is different in $$S_2$$ from the motion in $$S_1$$.

 

[Pete]

It is a little more complicated than that, see here.

Again, you're thinking of a wheel rolling at relativistic speed relative to a surface, ie one that is both moving relativistically and spinning relativistically.

This wheel is rolling very slowly relative to a fast moving surface - it is moving relativistically, but not spinning relativistically.

True but , among all these things, it gives the correct formalism of the rolling circle against the straight line trajectory. Ignore the raytracing part, if you look at the animations (pick the first one) it shows how the markers on the wheel line up with the markers on the ground).

Well, it gives pretty animations and I'm sure the underlying formalism is correct, but no formalism is actually given that I can see (maybe I didn't dig far enough), so it won't help Zeno much.

 

[Tach]

Again, you're thinking of a wheel rolling at relativistic speed relative to a surface, ie one that is both moving relativistically and spinning relativistically.

Doesn't matter, you need to solve a problem of relativistic kinematics either way. You can't solve the problem for a snapshot of the wheel, the way Zeno does.

This wheel is rolling very slowly relative to a fast moving surface - it is moving relativistically, but not spinning relativistically.

Consider v the composition of the speed of the center of the wheel wrt $$S_1$$ and the speed of $$S_2$$ wrt $$S_1$$.

Well, it gives pretty animations and I'm sure the underlying formalism is correct, but no formalism is actually given that I can see (maybe I didn't dig far enough), so it won't help Zeno much.

Look inside their papers.

 

[Pete]

Doesn't matter, you need to solve a problem of relativistic kinematics either way. You can't solve the problem for a snapshot of the wheel, the way Zeno does.

Sure, but Zeno did give the correct equation for the snapshot itself.

Consider v the composition of the speed of the center of the wheel wrt $$S_1$$ and the speed of $$S_2$$ wrt $$S_1$$.

In this case the speed of the center of the wheel wrt S1 is approaching zero.

Look inside their papers.

Can you be more specific?

 

[Tach]

Sure, but Zeno did give the correct equation for the snapshot itself.

I don't think that the snapshot is useful in solving this problem, this is a kinematics problem, not a geometry problem.

In this case the speed of the center of the wheel wrt S1 is approaching zero.

But it isn't zero, the wheel needs to roll. You need to figure out how the markers on the wheel line up with the markers on the ground when the wheel is rolling

 

[OnlyMe]

Zeno's posted problem is about a wheel rolling slowly relative to the surface, but considering a reference frame in which the surface is moving relativistically. And we're not concerned with the perceptual artefacts.

Both the surface and the wheel would have a relativistic linear velocity, and are length contracted in the line of relativistic motion only. The circumference of the resulting elliptical wheel is in this case an perceptual artifact, as pete mentions.

Accepting that Lorentz contractions for moving objects are real, only the relativistic linear motion would result in a length contraction. And that would be as far as the wheel is concerned a continuous event in the line of relativistic motion only. That portion of the wheel's circumference that is not length contracted cannot be used as a measure of the distance traveled as the wheel rolls/turns...

The only way I see to use the circumference of the wheel to compute the distance, would be to discard the perceptual artifact Pete mentioned and attempt to calculate a length contracted circumference. This would have to exclude the un-contracted diameter of the wheel perpendicular to its relativistic motion, relying only on the length contracted diameter as only that portion of the circumference associated with the length contracted diameter actually rolls along the length contracted surface. For the wheel length contraction occurs as a continuous event, in line with its relativistic motion.

Though to an outside stationary observer the wheel would appear to be elliptical and length contracted in only one direction, that portion of the circumference of the wheel in contact with the surface is always length contracted exactly the same as is the surface.

 

[Pete]

I don't think that the snapshot is useful in solving this problem, this is a kinematics problem, not a geometry problem.

It is correct that the snapshot isn't directly useful, as pointed out to Zeno in the first reply, but this extended diversion has been about whether Zeno's snapshot equation of the ellipse is correct - which it is.

And this is definitely a geometry problem, as demonstrated below.

But it isn't zero, the wheel needs to roll. You need to figure out how the markers on the wheel line up with the markers on the ground when the wheel is rolling

The rolling in this scenario is not relativistic. We don't need a relativistic analysis to determine the distance traveled by the wheel in the rest frame of S2 - it is simply equal to the wheel's circumference.

The resources you linked to are specifically about relativistic rolling, they describe a wheel rolling relativistically on a stationary surface, so that the rim has relativistic speed in the inertial reference of the axle.

In this scenario, the speed of the rim is not relativistic in the inertial reference frame of the axis. It is a significantly different situation. For example, the rolling wheel in this thread has straight spokes in all reference frames(within any desired non-zero error). It does not look like this (from your spacetimetravel.org link):

In fact, the scenario in this thread could be conducted without any rolling at all:

Consider a wheel on a surface.
In frame S1:

• The surface is at rest
• The wheel is at rest
• The surface is tangential to the wheel's perimeter
• The wheel is circular with diameter 10 units.
• The circumference of the wheel is 31.4 units
• There are two lines marked on the surface, parallel to the wheel's axis.
• The distance between the two lines is 31.4 units
• The distance between the two lines is the same as the circumference of the wheel
• A rope that is just long enough to reach from one line to the other will also be just long enough to wrap once around the wheel.

In frame S2:

• The x axis is parallel to the surface and perpendicular to the wheel's axis.
• The y axis is perpendicular to the surface and perpendicular to the wheel's axis.
• The wheel and surface are moving at 0.8c parallel to the x axis.
• The shape of the wheel is congruent to the ellipse described by
  $$\frac{25 x^2}{9} + y^2 = 25$$
• The circumference of the wheel is 25.9 units
• The distance between the two lines is 18.8 units
• The distance between the two lines is not the same as the circumference of the wheel

Everything so far is correct, right?

The only problem is in Zeno's final conclusion:

• A rope that is just long enough to reach from one line to the other will not be long enough to wrap once around the wheel.

Do you see that this problem is not about relativistic rolling at all, but rather about how length contraction changes with orientation to the velocity vector?

 

[Pete]

Both the surface and the wheel would have a relativistic linear velocity, and are length contracted in the line of relativistic motion only. The circumference of the resulting elliptical wheel is in this case an perceptual artifact, as pete mentions.

Well, the perceptual artifacts I mentioned were the different time lags between light scattered of different parts of the wheel reaching an observer's eye or camera, as simulated in the link Tach provided.

So the elliptical shape of the wheel and its circumference is not a perceptual artefact in that sense.

The only way I see to use the circumference of the wheel to compute the distance, would be to discard the perceptual artifact Pete mentioned and attempt to calculate a length contracted circumference. This would have to exclude the un-contracted diameter of the wheel perpendicular to its relativistic motion, relying only on the length contracted diameter as only that portion of the circumference associated with the length contracted diameter actually rolls along the length contracted surface. For the wheel length contraction occurs as a continuous event, in line with its relativistic motion.

You could maybe do an integral where the length of each element is adjusted to what its length will be when it meets the surface, such as:
$$\begin{align}
\frac{25x^2}{9}+y^2 &= 25 \\
(dc')^2 &= (dx)^2 + (\frac{dy}{\gamma})^2 \\
c' &= 4\int\nolimits_{x=0}^{x=3}dc'
\end{align}$$

But that's as about as far as I can go, and I'm not completely confident of that.

 

[OnlyMe]

Well, the perceptual artifacts I mentioned were the different time lags between light scattered of different parts of the wheel reaching an observer's eye or camera, as simulated in the link Tach provided.

So the elliptical shape of the wheel and its circumference is not a perceptual artefact in that sense.

I apologize for the mis-quote.

On re-reading my own post it seems a bit confused.

My confusion came from considering observers in both the relativistic frame and a stationary frame of reference. From within the relativistic frame of reference an observer would not "see" the wheel as an ellipse. From an at rest frame it would "appear" to be an ellipse. I had added, Accepting that Lorentz contractions for moving objects are real... since even though there is evidence to support time dilation, I cannot think of any proof of length contraction at or greater than everyday scales.

The basic point I was trying to make is that whether the wheel actually becomes length contracted or just appears to be, that portion of the wheel in contact with the surface is the only portion of its circumference that is relevant, as it would always be length contracted the same as the surface it rolls on. The elliptical wheel never rolls. The ellipse is always oriented 90 degrees to the length contraction. The circumference of the ellipse continually moves through varying degrees of length contraction, as the wheel rolls.

However, most of the conversation has been focused on other aspects of the thought experiment and would not be significantly altered by this detail.

These are good conversations that tend to make one think.... That is a good thing.

 

[Tach]

Consider a wheel on a surface.
In frame S1:

• The surface is at rest
• The wheel is at rest
• The surface is tangential to the wheel's perimeter
• The wheel is circular with diameter 10 units.
• The circumference of the wheel is 31.4 units
• There are two lines marked on the surface, parallel to the wheel's axis.
• The distance between the two lines is 31.4 units
• The distance between the two lines is the same as the circumference of the wheel
• A rope that is just long enough to reach from one line to the other will also be just long enough to wrap once around the wheel.

Correct

In frame S2:

• The x axis is parallel to the surface and perpendicular to the wheel's axis.
• The y axis is perpendicular to the surface and perpendicular to the wheel's axis.
• The wheel and surface are moving at 0.8c parallel to the x axis.
• The shape of the wheel is congruent to the ellipse described by
  $$\frac{25 x^2}{9} + y^2 = 25$$
• The circumference of the wheel is 25.9 units
• The distance between the two lines is 18.8 units

• 
  
  This part is not correct. This is not a pure geometry problem, it is a kinematics problem, so the speeds play a major role.
  In frame $$S_1$$ the center of wheel moves at speed $$v$$.
  
  The wheel will fit into the length of the rocket a number $$N_1$$ of times, where
  
  $$N_1=\frac{L_1-2R/ \gamma(v)}{2R/ \gamma(v)}=\frac{L_1 \gamma(v)}{2R}-1$$
  
  You must subtract $$R$$ from each end of the rocket.
  
  
  
  In frame $$S_2$$ the situation is a little more complicated, since $$S_1$$ moves at speed $$V$$ wrt $$S_2$$ while the wheel center moves at speed $$v$$ wrt $$S_1$$:
  
  $$N_2=\frac{L_2-2R/ \gamma(w)}{2R/ \gamma(w)}=\frac{L_1 \gamma(w)}{2R \gamma(V)}-1$$
  
  where $$w=\frac{v+V}{1+vV/c^2}$$
  
  
  
  
  Now, $$\gamma(w)=\gamma(v) \gamma(V) (1+vV/c^2)$$
  
  so:
  
  $$N_2=\frac{L_1 \gamma(v) (1+vV/c^2)}{2R}-1$$
  
  This means that $$N_2>N_1$$. They are equal if and only if $$v=0$$ (i.e. the wheel doesn't move in $$S_1$$, which is absurd since it contradicts the OP) or if $$V=0$$ (which reduces the problem to a trivial one). This should not be surprising since , from the perspective of frame $$S_2$$ the wheel needs to "chase" after the far end of the rocket (the far end of the rocket moves away from the wheel as the wheel rolls towards it). In order to get the number of revolutions, one simply needs to divide the numbers above by $$\pi$$. (added for Pete's benefit).

 

[Pete]

In frame S1:

• The wheel is at rest

Correct

...

In frame $$S_1$$ the center of wheel moves at speed $$v$$.

I don't think you're paying attention, Tach. The scenario I posted is illustrating Zeno's argument without any rolling at all.

 

[Pete]

In frame $$S_1$$ the center of wheel moves at speed $$v$$.
The wheel center moves a distance $$2R$$ while the perimeter rolls on the rocket $$S_1$$ floor a distance $$ 2 \pi R$$.

The wheel will do a number $$N_1$$ of revolutions, where

$$N_1=\frac{L_1-2R/ \gamma(v)}{2R/ \gamma(v)}=\frac{L_1 \gamma(v)}{2R}-1$$

You must subtract $$R$$ from each end of the rocket.



In frame $$S_2$$ the situation is a little more complicated, since $$S_1$$ moves at speed $$V$$ wrt $$S_2$$ while the wheel center moves at speed $$v$$ wrt $$S_1$$:

$$N_2=\frac{L_2-2R/ \gamma(w)}{2R/ \gamma(w)}=\frac{L_1 \gamma(w)}{2R \gamma(V)}-1$$

where $$w=\frac{v+V}{1+vV/c^2}$$

Surprisingly, $$N_1$$ and $$N_2$$ aren't equal. They are equal if and only if $$v=0$$ (i.e. the wheel doesn't move in $$S_1$$, which is absurd).

Congratulations, Tach, you've made your very own special relativity paradox!

 

[Tach]

I don't think you're paying attention, Tach. The scenario I posted is illustrating Zeno's argument without any rolling at all.

I have been paying a lot of attention, it appears that you are the one who refuses to listen. The wheel needs to roll in $$S_1$$ in order to get from one end of the rocket to the other one:

Inside S1 we have a 10 inch diameter bicycle tire rolling along the ground.
We have a spaceship called S1 moving past another spaceship called S2.

 

[Pete]

Tach, I'm suggesting a modified scenario, in which the wheel does not move along the rocket.

Here, read it again. Remember, this is not supposed to be the same scenario as in the original post. In this scenario, the wheel is not rolling. But it still demonstrates what Zeno is thinking:

Consider a wheel on a surface.
In frame S1:

• The surface is at rest
• The wheel is at rest
• The surface is tangential to the wheel's perimeter
• The wheel is circular with diameter 10 units.
• The circumference of the wheel is 31.4 units
• There are two lines marked on the surface, parallel to the wheel's axis.
• The distance between the two lines is 31.4 units
• The distance between the two lines is the same as the circumference of the wheel
• A rope that is just long enough to reach from one line to the other will also be just long enough to wrap once around the wheel.

In frame S2:

• The x axis is parallel to the surface and perpendicular to the wheel's axis.
• The y axis is perpendicular to the surface and perpendicular to the wheel's axis.
• The wheel and surface are moving at 0.8c parallel to the x axis.
• The shape of the wheel is congruent to the ellipse described by
  $$\frac{25 x^2}{9} + y^2 = 25$$
• The circumference of the wheel is 25.9 units
• The distance between the two lines is 18.8 units
• The distance between the two lines is not the same as the circumference of the wheel

The only problem is in Zeno's final conclusion:

• A rope that is just long enough to reach from one line to the other will not be long enough to wrap once around the wheel.

 

[Tach]

Tach, I'm suggesting a modified scenario, in which the wheel does not move along the rocket.

The solution I gave you is general, it includes your subcase. I stated very clearly that $$N_1=N_2$$ if and only if $$v=0$$ (your subcase).
You aren't solving Zeno's problem, you are solving a caricature version of his problem, I gave you the general solution.

The only problem is in Zeno's final conclusion:

A rope that is just long enough to reach from one line to the other will not be long enough to wrap once around the wheel.

There is no such statement in Zeno's post.

 

[Pete]

Tach, your "solution" clearly can't be right because it gives inconsistent results in different reference frames.

Your first mistake is here:

The wheel center moves a distance 2R while the perimeter rolls on the rocket S1 floor a distance 2 pi R.

You somehow have the wheel rolling further than the axis moves. Neat trick!