1 is 0.9999999999999............

[quantum_wave]

That's it.
So in that case, the 0.999..... isn't equal to 1, it is the wrong answer.
Wrong, even though it is the number that you get from the calculation.
The result is always inaccurate, no matter how many digits you put after the zero, even an infinite number.

No, because both .333... and .999... are notations, not the result of calculations. The notations have been defined. .333... is defined as equal to 1/3, and .999... is defined as equal to 1. We still don't have an equation that answers your earlier request.

 

[Undefined]

You haven't provided any "new approach". Just plain misconceptions.



There is no subtlety, contrary to your misconceptions both 0 and 0.(9) are numbers.

How would you know, since you don't read properly and fairly in full context, and so just default to generic catchphrases and personal insults (all things for which you have been rightly banned more than once before here and elsewhere)? Your 'bad habit' of willfully ignoring or kneejerking to any original ideas, points/suggestions and arguments presented by others is your signature problem, Tach. Your usual fallback of pretentiously resorting to stock phrases and spurious claims as if from authority are against the spirit of site rules for fair debate. You even fail to distinguish who said what in some cases, and end up attacking the wrong person! No wonder you get banned again and again. Get the message yet? Do better, Tach.

 

[Beer w/Straw]

RealityCheck.

You have an eloquent, dignified manner in posting. I am very interested in when I can expect your book on store shelves.

 

[elte]

Dividing 1 by 3 in longhand can help in looking at this problem.

 

[chinglu]

I don't know why this thread is here.

Anyway, if .9(n) emerges into 1, then since mathematics is a decidable science, it can be witnessed.

So, define a witness function W(n) = .9(n), which means n nines after the decimal point.

SURELY, since math is decidable, we can witness .9999... emerging into 1.

Yet, let's apply transfinite induction on all finite ordinals.

That means, to prove a property P(x), we establish $$\exists n\neg(P(n)) $$ is false.

Hence, $$\forall n (P(n)) $$ is true.

So, we want to know if there is any n in which W(n)= 1. Assume $$\exists n (W(n)=1) $$ is true.

Form the set $$B = \{ n:W(n)=1 \} $$. Since any set of ordinals has a least element, choose the least $$b \epsilon B $$.

Then, $$W(b)=1$$, which is a contradiction since .9(b) is finite and certainly not 1. Hence, we have established $$\forall n (W(n) \neq 1) $$

This proves after exhausting every natural number, we still do not have 1. Therefore, the witness function never sees 1 emerge from the sequence of 9's. Further, the proof above shows it is impossible to witness such an event even given all natural numbers. And, if some piece of math logic cannot be witnessed, then it is pure crackpottery or magic.

There is a similar proof in recursion theory. Assume an enhanced Turing machine with an unlimited stack register R2 and an unlimited index register R1.

The algorithm is below.

R2 := empty ;
R1 := 0;

do {
if ( *R1 == 0 )
push(R2, ".");
else
push( R2, "9");
++R1;
while ( R2 != 1 ) ;


Note that the algorithm never ends. Thus, R2 never becomes 1.

 

[kwhilborn]

@ Chinglu,

a) Take 1
b) divide it by 3

now try and make it one again using your answer of 0.333...

Does this mean we cannot get back to the original number 1?

If you use fractions it is possible 1/3 + 1/3 + 1/3 = 3/3 = 1

Now show us how to do it with decimal.

 

[chinglu]

@ Chinglu,

a) Take 1
b) divide it by 3

now try and make it one again using your answer of 0.333...

Does this mean we cannot get back to the original number 1?

If you use fractions it is possible 1/3 + 1/3 + 1/3 = 3/3 = 1

Now show us how to do it with decimal.

The proof demonstrates you can't divide 1 by 3 and get one number.

It is a finite sequence for any index n of the division. I'll leave it to you to devise a witness function to verify/witness every division by the Euclidean algorithm such that there is a number of .333 infinite. You will note you will only witness a finite number of divisions or arrive at a contradiction.

Try it using my logic above.

 

[kwhilborn]

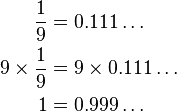
Wikipedia

Ed Dubinsky's APOS theory of mathematical learning, he and his collaborators (2005) propose that students who conceive of 0.999... as a finite, indeterminate string with an infinitely small distance from 1 have "not yet constructed a complete process conception of the infinite decimal". Other students who have a complete process conception of 0.999... may not yet be able to "encapsulate" that process into an "object conception", like the object conception they have of 1, and so they view the process 0.999... and the object 1 as incompatible. Dubinsky et al. also link this mental ability of encapsulation to viewing 1⁄3 as a number in its own right and to dealing with the set of natural numbers as a whole.[41]
In popular culture[edit]

With the rise of the Internet, debates about 0.999... have escaped the classroom and are commonplace on newsgroups and message boards, including many that nominally have little to do with mathematics. In the newsgroup sci.math, arguing over 0.999... is described as a "popular sport", and it is one of the questions answered in its FAQ.[42] The FAQ briefly covers 1⁄3, multiplication by 10, and limits, and it alludes to Cauchy sequences as well.

This is why you are in the fringe area. I am a Geologist and not a Mathematician, but I can grasp that a 0.99999 number continuing to infinity can be too close to ignore.

It is a common argument, but imagination is required to process conception of the infinite decimal. Infinity is further than anyone can imagine so there needs to be a leap of faith.

 

[Undefined]

Hi kwhilborn. Just surfing through and checking PMs, and I saw your above argument.

That just effectively brings the question back further; to:

What does the NOTATION form "0.11111..." equal?

Once you use the "..." to indicate an unfinished division, then you are making the NOTATION/DEFINITION (via some 'limits' argument using an infinity symbol or whatever) that the "0.111..." "will equal" whatever number you say it does.

So, what does "0.1111..." equal in your view?

See? If you are just trivially manipulating the NOTATION rather than a real number, then you just move the issue from "0.9999..." notation to "0.1111..." notation, and your above manipulation is equally trivial because it does not have any argument different from those you made for the "0.9999..." notation form.

As quantum_wave points out, it is DEFINED by convention, and not the direct 'output value' number from an actual numerical calculation/action as such.

Finished surfing through. Logging out again. Bye and good luck, kwhilborn, everyone.

 

[TruthSeeker]

0.999999... does not equal 1. Two different numbers. 0.99999... is just a tiny little bit too small to be 1. Otherwise we would just use "1" to convey the "0.99999..." information. It's just a language, a system of communication, with pretty straightforward rules. Very simple.

 

[kwhilborn]

@ undefined,

There is a reason this topic was moved to the Fringe alternative theories section. The photo depicting 0.111... X 9 was taken directly from Wikipedia concerning this very common argument.

I do not understand how you think 0.111... can equal any number? It has parameters.

You said,

As quantum_wave points out, it is DEFINED by convention, and not the direct 'output value' number from an actual numerical calculation/action as such.

Duh! I have already said it was defined by convention when I said ,

a 0.99999 number continuing to infinity can be too close to ignore.

and

imagination is required to process conception of the infinite decimal. Infinity is further than anyone can imagine so there needs to be a leap of faith.

It is convention based on wisdom that decided that 0.99999... continued to the end of the universe and back again in an infinite loop is close enough to 1 to be considered such.

Let me put it another way.

Try to subtract 0.999... from 1. Your answer will start as 0.000000000000000000 and will try to catch the infinity of it all.

So....

The difference between the two numbers is 0.000... continued to infinity places followed by a one. Now how can we even write such a number? We have 0.000... continuing for infinity with a one at the end of it, but there is no end to it. The only way to conceive of this number is to say 0.000... = 0.

Some might "Define by convention" that they are equal enough for the girls I date. Check wikipedia for when this leap of faith occurred and who first accepted the actuality of it.

0.9999 does not equal 1, but 0.999... continued forever does. This is accepted by convention as has been said.

 

[arfa brane]

A equal to B is not necessarily the same as A equivalent to B.

Equality is a form of equivalence, but there are a lot of other equivalences than A = B.

 

[Tach]

How would you know, since you don't read properly and fairly in full context,

easy, I see your fringe claims that 0 and 0.(9) "are not numbers". Elementary arithmetic says the opposite.

What does the NOTATION form "0.11111..." equal?

$$\frac{1}{10}+\frac{1}{10^2}+.....$$

It represents a series of powers (convergent). And , yes, it is a number, contrary to your misconceptions.

 

[Trippy]

No, because both .333... and .999... are notations, not the result of calculations. The notations have been defined. .333... is defined as equal to 1/3, and .999... is defined as equal to 1. We still don't have an equation that answers your earlier request.

I think you need to refresh your memory on long division and try again...

 

[Sarkus]

I remember doing a "proof" for this at school - but my understanding may be woeful in the grand scheme of things.
Anyhoo...

X = 0.99999.....
10X = 9.999999....
10X - X = 9
9X = 9
X = 1

Therefore X = 1 = 0.9999....

QED

The key, I guess, is in accepting that 0.999.... multiplied by 10 is 9.999....
And at the level of maths I was told this "proof", we had no reason to dispute the idea.

 

[quantum_wave]

I think you need to refresh your memory on long division and try again...

Are you saying that 1 divided by 3 is .333...? If so, I am saying that ".333..." is a notation that represents the result of 1 divided by 3. Let me clarify that ".333...", i.e. a short sequence of threes followed by "..." is a short hand notation that is defined to equal 1/3, while 1 divided by 3 actually is a decimal point followed by an infinite sequence of threes.

 

[TruthSeeker]

10X = 9.999999....
10X - X = 9

That's incorrect, it makes no sense. If you were to subtract x from one side, you would have to do the same with the other.

10x = 9.99999...
10x - x = 9.99999... - x

The key, I guess, is in accepting that 0.999.... multiplied by 10 is 9.999....

There is nothing wrong with that part.

 

[Quantum Quack]

This has been discussed over and over.

However, there are some proofs in set theory in which this does not hold.

For example, use transfinite induction on only natural numbers.

So, we seek the least index n such that .9(n) = 1. We find it cannot be decided since for all indexes n, .9(n) != 1. This is a problem.

We also also can take an approach of considering a neighborhood around 1. We also see for all n, we can find a number between .9(n) and 1.

We can't find any natural number in which this relation is false. So, if we could actually exhaust all n, we are left in the state there is a number between .9(n) and 1. This actually means we cannot exhaust all n.

I hope we can see discussion on this issue.

to me this all boils down to the question of :

Does:

(1/infinity) = 0

re: Zeno's paradox

Achilles and the tortoise



(subscribing)

 

[chinglu]

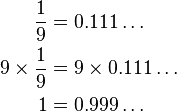
Wikipedia



This is why you are in the fringe area. I am a Geologist and not a Mathematician, but I can grasp that a 0.99999 number continuing to infinity can be too close to ignore.

It is a common argument, but imagination is required to process conception of the infinite decimal. Infinity is further than anyone can imagine so there needs to be a leap of faith.

Really, I provided the induction.

Tell me what n .9(n) becomes 1? When you figure out there is no such n, then you must show how .9(n) magically emerges into 1 when for all n that is false.

See, there is no leap of faith possible. For all natural numbers, the statement is false. So, what else are you going to use other than magic?

 

[chinglu]

easy, I see your fringe claims that 0 and 0.(9) "are not numbers". Elementary arithmetic says the opposite.



$$\frac{1}{10}+\frac{1}{10^2}+.....$$

It represents a series of powers (convergent). And , yes, it is a number, contrary to your misconceptions.

Really, at which n is it the same number when for all n it is a different number.

Show me a valid argument by induction where your series is only 1 specific number.