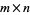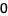Yang–Mills and Mass Gap

[arfa brane]

Back to determining the Lie algebra over the trivial group U(1), as the isomorphism SO(2) as a set of 2 x 2 matrices.

So I can write: $$ M(\theta) = I cos\theta + iXsin\theta $$, where the matrices I and X are as set out in post 119.

Now I expand $$ cos\theta,\; sin\theta $$, and I have:

$$ M(\theta) = I(1 - \frac {\theta^2} {2!} + \frac {\theta^4} {4!} + ... ) + iX(\theta - \frac {\theta^3} {3!} + \frac {\theta^5} {5!} + ... ) $$

$$ = I + i \theta X + \frac {(i\theta X)^2} {2!} + \frac {(i\theta X)^3} {3!} + ... $$,

since $$ X^{2n} = I $$, and $$ X^{2n + 1} = X $$, for n = 1,2,3 ...; and of course powers of i alternate: even powers are ±1, odd powers are ±i.

But this is the Taylor expansion of $$ e^{i\theta X} $$! Hence, X is called the generator of the Lie group.

Not quite there yet . . .

 

[arfa brane]

Now I want to show that the matrix: $$\begin{pmatrix} 0 & -1 \\ 1 & 0\end{pmatrix} $$ is the first derivative of $$ M(\theta) = \begin{pmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{pmatrix} $$, when evaluated at $$ \theta = 0 $$.

So, $$ \frac {d} {d\theta} \begin{pmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{pmatrix} = \begin{pmatrix} -sin \theta & -cos \theta \\ cos \theta & -sin \theta \end{pmatrix} $$.

And $$ \begin{pmatrix} -sin \theta & -cos \theta \\ cos \theta & -sin \theta \end{pmatrix}_{\theta = 0} = \begin{pmatrix} 0 & -1 \\ 1 & 0\end{pmatrix} = M'(0)$$.

Hence, $$ X = -i M'(0) $$.

The other step involves a Taylor expansion of $$ M(\theta) $$ around $$ \theta = 0 $$, or a Maclaurin series.

Which is: $$ M(\theta) = I + \theta M'(0) + \frac {\theta^2M''(0)} {2!} + \frac {\theta^3M''(0)} {3!} +\; ... $$

Then we can see that, if $$ \theta $$ is really small, the series is approximately: $$ I + \theta M'(0) = I + i\theta X $$ (higher order terms are negligibly small).

. . . and that's more or less it. As $$ \theta $$ gets smaller and approaches an infinitesimal value, the approximation gets closer.
As to an adjoint representation, I think that's only relevant when there is more than one parameter for the Lie group (or alternatively, the representation is its own adjoint?).

 

[NotEinstein]

I've already given at least one example earlier, but sure, here's another one: let's say a sphere rotates once per hour. 1 hours is 60 minutes, so $$T=60$$, which is larger than $$1$$. QED.

Hansda, can I interpret your silence on this matter as an admission of your error?

 

[arfa brane]

I think hansda is somewhat confused about how frequency and the period are related in oscillatory motion.

In particular, what difference it makes to the relation when you choose some scale, such as minutes or seconds (the answer is, no difference at all).
A frequency (or period) of "one" is physically meaningless.

 

[arfa brane]

More Wiki stuff:

Lie algebras

Given a Lie group G and its associated Lie algebra $$\mathfrak {g} $$, the exponential map is a map $$\mathfrak {g} $$ ↦ G satisfying similar properties.

In fact, since R is the Lie algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(n,R) of invertible n × n matrices has as Lie algebra M(n,R), the space of all n × n matrices, the exponential function for square matrices is a special case of the Lie algebra exponential map.

The identity exp(x + y) = exp(x)exp(y) can fail for Lie algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.

--https://en.wikipedia.org/wiki/Exponential_function

In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group.

Let X be an n×n real or complex matrix. The exponential of X, denoted by $$ e^X$$ or exp(X), is the n×n matrix given by the power series $$ e^{X}=\sum _{k=0}^{\infty }{1 \over k!}X^{k} $$, where $$ X^{0}$$ is defined to be the identity matrix $$ I $$ with the same dimensions as $$ X $$.[1]

--https://en.wikipedia.org/wiki/Matrix_exponential

It's interesting that also $$ e^{0_n} = I_n $$, where $$ 0_n $$ is the n × n 0-matrix. This implies that $$ X^{0} = e^{0_n} $$, when X is any n × n matrix (and the power of X is zero, of course).

Perhaps rpenner's posts about matrix exponentials shed some light on this?

 

[QuarkHead]

I really don't understand why you are here, arfa. In post #116 I told you that the exponential map recovers a Lie group frm its algebra. Now are repeating this fact by quoting the Wiki! Why ignore the help being offered here?

Furthermore it is quite untrue that $$e^0 $$ implies a $$0 \times 0 $$ matrix. Rather it implies a matrix with zero trace which implies it is an element in the algebra associated to a group with unit determinant via $$e^0=1 $$ where $$detA=e^{trX}$$ for any $$A \in G$$ and some $$X \in \mathfrak {g}$$

 

[arfa brane]

Furthermore it is quite untrue that $$ e^0$$ implies a 0×0 matrix.

What's a 0x0 matrix?
Any number, e is a number, with an exponent of 0 is equal to 1, as far as I understand it. But if a number is defined as a 1x1 matrix, then a nxn matrix with exponent of 0 is the nxn identity matrix. That all seems quite logical.

What changes when the 1x1 matrix is e, and the exponent is a nxn 0-matrix?

 

[QuarkHead]

Oops

 

[QuarkHead]

What changes when the 1x1 matrix is e, and the exponent is a nxn 0-matrix?

There is no such thing as a n x n 0-matrix.

 

[arfa brane]

A zero matrix is an

matrix consisting of all 0s (MacDuffee 1943, p. 27), denoted

. Zero matrices are sometimes also known as null matrices (Akivis and Goldberg 1972, p. 71).

--http://mathworld.wolfram.com/ZeroMatrix.html
??

I assume it's ok that m = n, for m x n, so that the zero matrix happens to be a square matrix.

Also

In post #116 I told you that the exponential map recovers a Lie group frm its algebra.

That's also what McKenzie has to say about it. And I have seen all this before, back in 2003 or so, except the matrix exponential wasn't explained in terms of a generator (or an element of a Lie algebra). Back then it was about a way to generate rotations of fermion spin, and the algebraic element was a Pauli matrix. It seemed then to be about generating an approximation, by restricting the angle to be small enough.

Now are repeating this fact by quoting the Wiki! Why ignore the help being offered here?

I'm just posting, let's call it "supporting evidence". In the interests of clarity and exposition . . . (given that your or my expositories aren't necessarily all that enlightening to other people)

 

[hansda]

I think hansda is somewhat confused about how frequency and the period are related in oscillatory motion.

The relation is simple. It is $$ fT=1$$ or $$f=\frac{1}{T} $$ .

In particular, what difference it makes to the relation when you choose some scale, such as minutes or seconds (the answer is, no difference at all).
A frequency (or period) of "one" is physically meaningless.

A frequency of "one" relates to maximum time period, for any given interval of time in seconds or minutes or whatever units of time are chosen; over which the frequency is to be measured.

 

[origin]

I think hansda is somewhat confused about how frequency and the period are related in oscillatory motion.

Handsa apparently wants to leave no doubt that he is confused so he wrote:

The relation is simple. It is $$ fT=1$$ or $$f=\frac{1}{T} $$ .
A frequency of "one" relates to maximum time period, for any given interval of time in seconds or minutes or whatever units of time are chosen; over which the frequency is to be measured.

Frequency is the reciprocal of the period. That is all there is to it.

 

[NotEinstein]

A frequency of "one" relates to maximum time period, for any given interval of time in seconds or minutes or whatever units of time are chosen; over which the frequency is to be measured.

So you stick to your claim (without providing any proof for it, even after having repeatedly been asked for that) that something that is rotating around an axis must do so with at least 1 full rotation per picosecond. That means that either the Earth isn't rotating, or a full sunrise-sundown-sunrise day lasts at most a picosecond... As that seems to be quite fringy to me, I guess it's time this entire discussion is split off of this thread, and moved to pseudo-science, where it clearly belongs?

 

[arfa brane]

Ok, this thread isn't going anywhere fast (or it seems, at any speed less than that).

I'll hand over to yet another link to a book written by none other than Howard Georgi, he of the Georgi-Glashow SU(5) "Grand Unified Theory".

Reading through just the first chapter though, it (the book) seems to go pretty fast. Irreducible representations appear on page 5, for instance. I did a one semester course on abstract algebra (what they let you study after 2 years of linear algebra), and we didn't really get into continuous groups much, or representation theory either.

So just a heads up; this online book is not for beginners. If you want some insights into Yang-Mills and so on, then this book is the territory.

 

[QuarkHead]

Ok, this thread isn't going anywhere fast (or it seems, at any speed less than that).

And you still don't understand why, do you?

Let me explain again. This is a discussion forum. That means that people come here to discuss ideas, mostly in science, and try to contribute their own knowledge. It is not an internet link exchange, still less is it a place to paraphrase poorly understood random articles from the 'net.

I'll hand over to yet another link

Yet more proof that you just don't get it.

You effectively killed thIs thread for this reason.

 

[arfa brane]

I think not only is this thread dead, the entire forum is pretty much. There isn't much science being discussed, and we have people being condescending at best.

For example:

Why ignore the help being offered here?

. Say what? I'm supposed to believe sciforums has a poster who's the ultimate arbiter, I don't have to look anywhere else? What exactly gives this poster the idea I'm ignoring them anyway? I really don't get it.

"Poorly understood random articles", my ass.

 

[arfa brane]

. . . a matrix with zero trace which implies it is an element in the algebra associated to a group with unit determinant via $$ e^0 = 1 $$ where $$ detA = e^{trX} $$ for any A ∈ G and some X ∈ [the algebra] .

.

The set of n x n matrices is a subset of the set of all m x n matrices. I can easily define an additive group of n x n matrices over the integers, say: $$ (\{M_{ij}| \delta_{ij} = 1, M_{ab} \in \mathbb {Z}\},\; +) $$. The identify of this group is the n x n zero matrix (0-matrix). There is such a thing.

And, $$ detM = e^{trX} $$ when X is the additive identity, i.e. $$ e^X = I $$; this is trivially true because all the terms in the Taylor expansion except the first, are the zero matrix.

 

[arfa brane]

Oops, that should be the set: $$\{M_{ij}| \delta_{ii} = n, M_{ab} \in \mathbb {Z}\}$$, where n is the dimension of any M. That means I interpret $$ \delta_{ii} $$ as a sum over equal indices.

Another way I could do it is to restrict i, j, and a, b to belong to the same index set.

 

[arfa brane]

So, any matrix can be decomposed into a sum of nonzero matrices, and we can easily see that, for a 2 x 2 matrix

$$ \begin{pmatrix} a & b \\ c & d \end{pmatrix} = a\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} + b\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} + c\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} + d\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} $$

We can also then write: $$ \begin{pmatrix} a & b \\ c & d \end{pmatrix} = a|1\rangle + b|2 \rangle + c[3\rangle + d|4\rangle $$, where $$ |k\rangle $$ is a vector. The coefficients might be integers, real or complex numbers, just about anything.

We could have that a 2 x 2 matrix is a rotation matrix,

$$ R = \begin{pmatrix} cos\phi & -sin\phi \\ sin\phi & cos\phi \end{pmatrix} = cos\phi (|1\rangle + |4\rangle) + sin\phi(|3\rangle - |2\rangle) $$.

Now I can, with a change of notation, have a slightly different looking map (another homomorphism from the "vector" space to itself), viz:

$$ R = cos\phi (|1\rangle + |2\rangle) + sin\phi(|\bar{1}\rangle - |\bar{2}\rangle) $$.

Looks more, erm, symmetric but it's the same representation.

Let's take an even simpler subset of this space, by restricting $$ \phi $$ to be an element of $$ \{\pi/2\,\; \pi,\; 3\pi/2(=-\pi/2),\; 2\pi\} $$; the rotational symmetries of a square.

 

[arfa brane]

Now, just for the hell of it, show that you can find a map from a space of unit vectors to a second space with the same 'structure', in that, in each of the spaces there is a way up to a scaling factor to join together n points with n unit vectors, and lets make the first space $$ \mathbb Z^2 $$ embedded in $$ \mathbb E^2 $$. This means there is a way to find a pair of unit vectors which are orthogonal, which means their inner product is 0 (the 1 x 1 zero matrix).

In the second space, there is half the angle between orthogonal directions, i.e. there is a map from $$ \phi $$ to $$ \phi/2 $$. A continuous map.

It's a matter of notation as to how this map can be represented, but we know what it looks like. It's a rotation matrix. The second $$ \mathbb Z^2 $$ maps the circle to half of itself so there's enough "room" for two copies in a full circle, or in other words, a function that wraps the circle twice (if a single wrapping is defined as "once around", which is all the points within the span of a rotating unit vector. In $$ \mathbb Z^2 $$, a line rotated away from say, (x,y) = (1,0) in a positive sense, will intersect another point in a square lattice which is "as far away from the identity" as you want it to be, well before the angle of rotation reaches a few degrees, there will be some point in the row of points corresponding to y = 1 that intersects the projected line.