Jarek Duda
Registered Senior Member
Electron is usually imagined as a simple point charge, but in fact it is a very complex entity:

- being electric charge itself means singular(-like?) configuration of electric field - E behaves like 1/r^2,
- it is also magnetic dipole moment - singular(-like?) configuration of magnetic field - B behaves like 1/r^3,
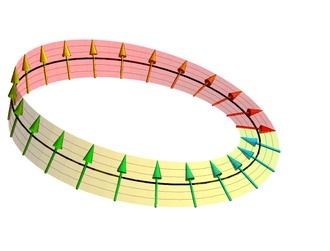
- it acts like a tiny gyroscope: attaching a force leads to response orthogonal to this force and to direction of gyroscopic moment, for example in Larmor precession,
- it has some internal oscillations - seen as zitterbewegung in Dirac theory, or as de Broglie's clock (E = mc^2 = hbar*omega), which can be directly observed (e.g. http://link.springer.com/article/10.1007/s10701-008-9225-1 ).
These properties suggest that electron is quite a complex entity - how to fit them into a perfect point? (physics doesn't like discontinuities as they would have infinite energy)
The electric field itself says that a single electron would affect the entire universe ... we could even say that this singular field defines the charge (can't we?), that electron is a configuration of the fields (what more is it?) - that it is a soliton of, among others, electromagnetic field.
So what does the popular claim that electron is a point means?
I understand it that the central singularity is perfect E ~ 1/r^2 ... however, calculating energy of such point singularity we get integrate of E^2*r^2 ~ 1/r^2, what is divergent in r = 0.
In other words - point charge would require infinite energy of electric field only - what is a nonsense as we know that 2 x 511keVs is sufficient to create electron-positron pair.
Another argument against point charge is running coupling - from https://en.wikipedia.org/wiki/Coupling_constant#Running_coupling
"In particular, at low energies, α ≈ 1/137, whereas at the scale of the Z boson, about 90 GeV, one measures α ≈ 1/127."
So alpha ~ charge^2 decreases for high energy collisions - the effective charge is reduced while particles are very close together.
Doesn't it suggest that the E ~ 1/r^2 is weakened very close to the center - additionally allowing to repair the problem with infinite energy.
Why electron is believed to be a point? What does it mean?
What would be expected if it wouldn't be?
Doesn't running coupling and infinite energy of point charge suggest that E ~ 1/r^2 is weakened for very small r?

- being electric charge itself means singular(-like?) configuration of electric field - E behaves like 1/r^2,
- it is also magnetic dipole moment - singular(-like?) configuration of magnetic field - B behaves like 1/r^3,
- it acts like a tiny gyroscope: attaching a force leads to response orthogonal to this force and to direction of gyroscopic moment, for example in Larmor precession,
- it has some internal oscillations - seen as zitterbewegung in Dirac theory, or as de Broglie's clock (E = mc^2 = hbar*omega), which can be directly observed (e.g. http://link.springer.com/article/10.1007/s10701-008-9225-1 ).
These properties suggest that electron is quite a complex entity - how to fit them into a perfect point? (physics doesn't like discontinuities as they would have infinite energy)
The electric field itself says that a single electron would affect the entire universe ... we could even say that this singular field defines the charge (can't we?), that electron is a configuration of the fields (what more is it?) - that it is a soliton of, among others, electromagnetic field.
So what does the popular claim that electron is a point means?
I understand it that the central singularity is perfect E ~ 1/r^2 ... however, calculating energy of such point singularity we get integrate of E^2*r^2 ~ 1/r^2, what is divergent in r = 0.
In other words - point charge would require infinite energy of electric field only - what is a nonsense as we know that 2 x 511keVs is sufficient to create electron-positron pair.
Another argument against point charge is running coupling - from https://en.wikipedia.org/wiki/Coupling_constant#Running_coupling
"In particular, at low energies, α ≈ 1/137, whereas at the scale of the Z boson, about 90 GeV, one measures α ≈ 1/127."
So alpha ~ charge^2 decreases for high energy collisions - the effective charge is reduced while particles are very close together.
Doesn't it suggest that the E ~ 1/r^2 is weakened very close to the center - additionally allowing to repair the problem with infinite energy.
Why electron is believed to be a point? What does it mean?
What would be expected if it wouldn't be?
Doesn't running coupling and infinite energy of point charge suggest that E ~ 1/r^2 is weakened for very small r?
Last edited: