The Monty Hall Problem Revisited

[DaveC426913]

phyti, humour me for a moment. Set aside theoretical and logical considerations and look at this from a fresh perspective. Look at the data of this actual sim.

Tell us where you think this sim is going wrong - give us a row number where any rule or probability is being violated.

Satisfy yourself that:
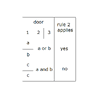
- the car is behind a random door for each of 200 games (column 2 is a sequence of randomly-chosen numbers 1-3)
- the user chooses a random door to start in each of 200 games (column 3 is a sequence of randomly-chosen numbers 1-3)
- Monty always opens a door that is not the player's choice or the car. In some games he gets to choose one of two doors, in other games he has only one door to open. (But this split result does not double the number of times it actually occurs.)
- the player always switches.

I dont mean a meta-analysis of what you think game "types" are or whatever a "composite" game might be. This is a list of 200 real, valid, independent games with 200 concrete outcomes. Literally, this could be the playbook of the last 200 episodes of the show.

Simply find any flaw in the data.


In fact, you surely don't have to review the entire list of 200; I've listed just the first 35 or so results. it has already converged on 2/3rds within the first twelve games or so.

By game twelve, the player's 'always switch' strategy has paid off eight times (i.e. 2/3rds).

Can you see why?

Feel free to run the sim yourself as many times as you want.



Are they random?

In this run of the sim:
Column 2: Car is
- behind door one 12/35 times,
- behind door two 11/35 times,
- behind door three 12/35 times.
Column 3: Player
- chooses door one 10/35 times,
- chooses door two 10/35 times,
- chooses door three 15/35 times.
Column 4: Monty opens a door
If player has chosen the door that has the car, Monty gets to open one of two doors (chosen randomly).
If player has not chosen the door that has the car, Monty has only one door he can open (since the other one has the car).
Column 5: Player switches:
Player always switches to the one remaining door.

 

[Sarkus]

'The player will only play either game 3 or 4 one third of the time'

There are 3 prizes behind any door location.
There are 4 host choices.
Do you know the difference?

Yes.
Do you?

The frequency of events, you know, that crucial little fact that you seem oblivious to, to the point of willful ignorance, is determined in the first place not by the host's choices, but by the player's choice.
You've been told this repeatedly.
You've ignored it repeatedly.

Stop wasting everyone's time.
You're either stupid or a troll. Heaven forbid you should even be a stupid troll.

 

[James R]

phyti:

This is ridiculous. I get the impression that you are refusing to even consider the various proofs and demonstrations that have been put in front of you. Instead, you're entirely focused on repeating the same flawed analysis over and over, while ignoring the fact that specific flaws in your reasoning have been pointed out.

Certainly, you have not worked through any of my proofs line by line to try to find a flaw. So, either you're too fixated on your own error to do that, or you're too lazy to try, or you're wilfully blinding yourself to disproofs of your claims, or you just don't have the brains for this stuff.

Whatever the problem is with you, it doesn't look like you're reachable. You need to engage with what I have posted to you - and that doesn't mean posting a three line dismissal of my analysis that doesn't actually grapple with any of the steps in my reasoning.

Repeating assertions that have already been disproved is intellectually dishonest. You need to respond to the specific objections raised to your analysis and to actually try to find flaws in the alternatives.

This problem isn't difficult. You can literally list all possible ways the game can play out, calculate the probability that the player will play each variant and then add up the probabilities of all variants in which switching doors results in a player win.

What you can't do is what you keep doing: ignoring the different probabilities of the player playing each game variant, and simply assuming that there is equal probability for each one. It's obtuse that you refuse to acknowledge the error that you have made.

Maybe you actually just don't understand the maths of probability. Maybe it's not wilful blindness, but just stupidity. Unfortunately, I have no cure for that, if that's the issue here.

 

[James R]

phyti:

JamesR;

If the census bureau issued a report stating the average family has 2.3 children, no one would expect to find .3 child in any randomly chosen home. The value 2.3 is a statistical average resulting from a large set of data studying family size. The value applies to the set and not to its individual elements. It typically does not correspond to anything in reality.

Probability is an abstract measure of success. It can be calculated as s/n, where s=number of successful events and n=number of possible events.
It is a substitute for knowledge.


View attachment 6706
From computer jargon, we compare the knowledge base or kb of the host to that of the player for a set of 5 doors as the game progresses.
A '1' means there is a car behind this door, a '0' means there is no car behind this door.
The host always knows the location of the car.
The player does not know the location of the car while guessing.
The player accepts 1 fact. The car is contained within the set of 5 doors which is a certainty with a value of 1. (There is no deception.)

For the kb tables, time advances downward. The player chooses door4.
To compensate for the player's empty kb, probability theory distributes the value of 1 uniformly as a value of 1/5 for each door. Both host and player know from experience, there is no 1/5 car behind any door. Now s/n=1/5.
The host opens door5, informing the player the car is not there. Now s/n=1/4.
The host opens door1, informing the player the car is not there. Now s/n=1/3.
The host opens door3, informing the player the car is not there. Now s/n=1/2.
As the host opens empty doors, n decreases, and the probability increases.
If the host opened the last empty door, then s/n=1. If it was the players 2nd choice
the host could open the player's 1st choice to verify the car was in the set of 5.
The host can open n-2 doors of the set regardless of the player's initial choice.

The game is dynamic and the possibilities and probabilities change as it progresses.
The idea that a probability has an independent existence after the start of the game is false. Probability is relative to the current circumstances, especially if they change.



NO!

Your analysis in this post is wrong, again. I anticipated this line of argument back in my post #148, and explained why it is wrong. Unfortunately, you chose to ignore that post.

I understand that the analysis in post #148 has a level of sophistication that is currently beyond you, given that you didn't understand the much simpler explanation in post #152 either.

I suggest that, if you want to make an honest attempt at following the arguments I have put to, at some point, you ought to forget about post #148 for now and concentrate on #152. After all, it's in that post where your error is most obviously exposed.

 

[James R]

phyti:

Just for completeness, here's the correct "player knowledge" table for your five-door example. If I were you, though, I'd stick to thinking about three doors, because your core error is more obvious in that case.

Player knowledge (i.e. probability that the car is behind each door as calculated by the player),
assuming the player chooses door 4 initially and the host knows the car is behind door 2.

Door 1    2    3    4    5
     0.2  0.2  0.2  0.2  0.2  Starting condition
     0    0.27 0.27 0.2  0.27 After host has opened door 1, revealing a goat.
     0    0.4  0.4  0.2  0    After host has opened door 5, revealing a goat.
     0    0.8  0    0.2  0    After host has opened door 3, revealing a goat.

At this point, the host offers the player the choice "Stay with door 4, or switch to door 2?"

Since the player in this case calculates that he has 4 times the chance of winning the car by switching his choice, compared to sticking with his initial choice, the player's best strategy is to switch doors, once again.

Of course, this "player knowledge" table would look identical for the game in which the car was actually behind door 4, the player initially chose door 4 and the host opened doors 1, 5 and 3 in the same sequence. But the player will only play this version of the game (the one in which he happens to choose the door with the car behind it, initially) in one game out of every five. So, although the "switch" strategy would lose in this case, the chance of losing is correctly predicted as 0.2 (equal to the probability, estimated by the player, that the car is actually behind door 4 at the time the player makes his initial choice of door).

 

[parmalee]

If the census bureau issued a report stating the average family has 2.3 children, no one would expect to find .3 child in any randomly chosen home. The value 2.3 is a statistical average resulting from a large set of data studying family size. The value applies to the set and not to its individual elements. It typically does not correspond to anything in reality.

??? And what exactly does this have to do withe the Monty Hall Problem?

 

[phyti]

Door 1 2 3 4 5
0.2 0.2 0.2 0.2 0.2 Starting condition
0 0.27 0.27 0.2 0.27 After host has opened door 1, revealing a goat.
0 0.4 0.4 0.2 0 After host has opened door 5, revealing a goat.
0 0.8 0 0.2 0 After host has opened door 3, revealing a goat.

Door 1 2 3 4 5
0.20 0.20 0.20 0.20 0.20 Starting condition
0.0 0.25 0.25 0.25 0.25 After host has opened door 1, revealing a goat.
0.0 0.33 0.33 0.33 0.0 After host has opened door 5, revealing a goat.
0.0 0.50 0.0 0.50 0.0 After host has opened door 3, revealing a goat.
0.0 1.00 0.0 0.0 0.0 After host has opened door 2, revealing a car

The player has no clue whether the car is behind door 2 or door 4. He guesses
The host opens door 2 informing the player he lost and the car was possible to win (fair game).
Notice the probability increases in a trend toward 1.
The reality of the game is, there is only 1 door containing a car.
Each door presents the same probability when you don't know.

 

[phyti]

forum;

Rule 1. Host cannot open the door from the player's 1st choice.
Rule 2. Host cannot open the door containing the car.

Player chooses door 1.
When car is not behind door 1 rule 2 applies.
When car is behind door 1rule 2 does not apply.
Rule 1has covered that condition.
Host needs 2 games to choose both doors.

 

[Sarkus]

Host needs 2 games to choose both doors.

But he doesn't get 2 games for each 1 of the other options! We've told you this, explained it to you numerous times in numerous ways. And still you ignore and continue your fallacious reasoning.
Your interpretation is that since the host needs 2 games to choose both doors, each of those games occurs as frequently as the other 2 games.
The correct interpretation is that the host picks those 2 doors each 50% of the time that that particular game is played, and that particular game is played 1/3 of the time. So each of the 2 sub-choices that the host makes within that game both have probability of 50% within that game - i.e. 1/6 chance each.

So, stop with your nonsense.
Please.

 

[DaveC426913]

A bunch of posts back he mentioned he's submitting a paper. That's why he's just vomiting explanation after explanation. And why hes not engaging. He's using this thread as a scratchpad to work out his paper.

 

[Sarkus]

A bunch of posts back he mentioned he's submitting a paper. That's why he's just vomiting explanation after explanation. And why hes not engaging. He's using this thread as a scratchpad to work out his paper.

It's a rather convoluted way of producing toilet paper, isn't it? Both end up full of shit, and need to be flushed.

 

[James R]

Door 1 2 3 4 5
0.2 0.2 0.2 0.2 0.2 Starting condition
0 0.27 0.27 0.2 0.27 After host has opened door 1, revealing a goat.
0 0.4 0.4 0.2 0 After host has opened door 5, revealing a goat.
0 0.8 0 0.2 0 After host has opened door 3, revealing a goat.

Door 1 2 3 4 5
0.20 0.20 0.20 0.20 0.20 Starting condition
0.0 0.25 0.25 0.25 0.25 After host has opened door 1, revealing a goat.
0.0 0.33 0.33 0.33 0.0 After host has opened door 5, revealing a goat.
0.0 0.50 0.0 0.50 0.0 After host has opened door 3, revealing a goat.
0.0 1.00 0.0 0.0 0.0 After host has opened door 2, revealing a car

The player has no clue whether the car is behind door 2 or door 4. He guesses
The host opens door 2 informing the player he lost and the car was possible to win (fair game).
Notice the probability increases in a trend toward 1.
The reality of the game is, there is only 1 door containing a car.
Each door presents the same probability when you don't know.

You're wrong again, phyti. Specifically, you haven't been careful about your statement "The player has no clue whether the car is behind door 2 or door 4". He has a clue at all times.

At the start of the game, the player knows that the car is behind one of the five doors, for sure. That's assuming the game is being played fairly by the host and the makers of the show. That the player does not know, at the start, is which of the five doors it is behind. We represent that state of knowledge by saying that there is a 0.2 probabilility for the car being behind each door. This is not about the actual state of affairs, remember. It is about the player's knowledge. The actual state of affairs is that the car is definitely behind one of the five doors and definitely not behind any of the other four doors.

More importantly, this is consistent with the player expecting that he will choose the "correct" door (the one with the car) once in every five times he plays the game, on average. And four times out of five he expects to choose the wrong door (one with a goat).

If the player has picked door 4 as his initial choice, the host will not open door 4 until after the player has made his choice to switch or stay. But the player knows that, in 4 games out of very 5 games he plays, he will have chosen the wrong door at the start, which means that he can expect to win the car at the end 4 times out of 5 by choosing to switch doors.

There's really nothing else that needs to be said about this. You have no refutation of this line of reasoning, so we don't even need to look at your many different ways of presenting the same erroneous analysis in various tables.

Anyway, why try to understand the 5 door version of the game, when you can't even get the 3 door version right?

 

[James R]

forum;

Rule 1. Host cannot open the door from the player's 1st choice.
Rule 2. Host cannot open the door containing the car.
View attachment 6715
Player chooses door 1.
When car is not behind door 1 rule 2 applies.
When car is behind door 1rule 2 does not apply.
Rule 1has covered that condition.
Host needs 2 games to choose both doors.

Two thirds of the time, the player will be playing a game in which he originally chose either door a or b. One third of the time, the player will be playing a game in which he originally chose door c.

If the player is playing a game in which he originally chose door a or b, he will win the game by switching. If he is playing a game in which he originally chose door c, he will lose the game by switching.

Therefore, the player wins two times out of every three plays by adopting the "switch" strategy.

This is what you need to grapple with. Why won't you do it?

 

[James R]

A bunch of posts back he mentioned he's submitting a paper. That's why he's just vomiting explanation after explanation. And why hes not engaging. He's using this thread as a scratchpad to work out his paper.

Good luck to him with the peer review process!

(Maybe he'll submit to a pay-to-publish junk journal, which will be the only type that will accept his nonsense.)

 

[James R]

phyti:

I have been thinking about your "player knowledge" table and mine for the 5 door game some more, in the minutes I have spent posting the above posts.

Door 1 2 3 4 5
0.2 0.2 0.2 0.2 0.2 Starting condition
0 0.27 0.27 0.2 0.27 After host has opened door 1, revealing a goat.
0 0.4 0.4 0.2 0 After host has opened door 5, revealing a goat.
0 0.8 0 0.2 0 After host has opened door 3, revealing a goat.

Door 1 2 3 4 5
0.20 0.20 0.20 0.20 0.20 Starting condition
0.0 0.25 0.25 0.25 0.25 After host has opened door 1, revealing a goat.
0.0 0.33 0.33 0.33 0.0 After host has opened door 5, revealing a goat.
0.0 0.50 0.0 0.50 0.0 After host has opened door 3, revealing a goat.
0.0 1.00 0.0 0.0 0.0 After host has opened door 2, revealing a car

The first table here is mine. The second one is yours.

Arguably, both tables are correct. It just depends on the assumptions we are both making.

We have assumed that these tables are supposed to represent a single playthrough of the game, for the specific case where the player initially chooses a door other than door 2 (I used door 4 for the player's initial choice in my table; for yours, the player's initial choice doesn't matter), and the car is actually behind door 2. But I assumed that my table actually represents the player's knowledge about how likely it is, over many plays of the game, that the car will be behind each door, whereas you assumed that the player is ignorant of the rules of the Monty Hall game.

Your analysis pretends that the player doesn't know the rules of the Monty Hall game. He doesn't know the rules restricting which doors the host is allowed to open. Since, in your analysis, there is no reason for the player to expect the host to be more likely to open, say, door 3 in the next step rather than opening door 4 (the one the player initially chose), the player has no valid reason to say that it is any more likely that the car is behind door 3 than behind door 4 at any stage of the single-play game.

My table, on the other hand, assumes that the player does know the rules of the game. He knows that the host is only allowed to open goat doors before giving him the choice of "switch or stay". He also knows that his initial pick of door (door 4, in the table) will only have the car behind it in one out of every five Monty Hall games that are played. So, he reasons that his initial pick of door 4 in this game has only a 1 in 5 (i.e. 0.2) chance of being correct, before the host starts opening doors.

Consider the first door opened by the host, then (door 1 in the table). The player knows the host was not allowed to open door 4. The host had to choose one of the doors 1,2,3 or 5. The host actually chose door 1, leaving doors 2,3,4 and 5 unopened.

What's the player's estimate of the probability that the car is behind door 2, after the host has opened door 1? Well, player knows that in 1 out of every 5 games, the car will be behind the door the player originally chose (door 4), and in 4 out of every 5 games the car will be behind one of doors 2,3 or 5. It follows that the probability calculated by the player after the host has opened the first door (door 1) is 1 in 5 for the car being behind door 4 (unchanged from the start of the game) and 4 in 5 for the car being behind of doors 2,3 or 5. The probability that the car is behind door 3, specifically, then is 4 in 5 divided evenly among the 3 options (doors 2,3 or 5), which gives 0.8/3 = 0.27 for door 3.

And so it goes for the rest of the table.

Bottom line, then, is: you assume a stupid player who doesn't know the rules of the Monty Hall game, while I assume a smart player who uses his knowledge of the rules to work out the probabilities each time the host opens a door.

The stupid player ignores available information about how the game is played and so ends up being faced with a 50-50 guess as to which door the car is behind. The stupid player can hope to win one game out of every two, on average.

The smart player, on the other hand, uses his knowledge of the rules to increases his chances of a win to 4 games out of 5, on average.

---
I should add that, in the original 3 door Monty Hall game, the smart player increases his chance of a win from 1/2 to 2/3 by adopting the "switch" strategy consistently. And in the 1 million door version of the game, the smart player can increase his chance of a win from 1/2 (50%) to 999,999/1,000,000 (99.9999%)

 

[parmalee]

@ James

Why don't you try your mind-reading thing on this guy? It seems that a lot of people here would like to know what is going on in phyti's head, and that includes me, as well.

 

[James R]

parmalee:

You are trolling. Stop it now.

 

[parmalee]

parmalee:

You are trolling. Stop it now.

For the record, I think that phyti is (also) trolling. Note that he has moved on from obsessing about the relevance and myriad possibilities with respect to the goats, to this fixation upon the host's choices. There is simply no way that he has read the countless responses and rebuttals to his "arguments" here and considered them. He is just making this shit up. (Or not. We can't really know, it just certainly seems that way.)

 

[Sarkus]

For the record, I think that phyti is (also) trolling.

Indeed. When someone writes such long posts but never addresses the actual correction that people provide, but just ignores it, dismiss it, and carries on, that's trolling. Relatively harmless, though, cos, well, it's not as though he sees someone correct him and immediately starts with the ad hominems.

Either way, the thread has gone on far longer than needed to address the issue, answer the questions, and identify that the poster has no interest in the corrections offered. Anything else here would just be ego-stroking, I'd have thought.

 

[parmalee]

Indeed. When someone writes such long posts but never addresses the actual correction that people provide, but just ignores it, dismiss it, and carries on, that's trolling. Relatively harmless, though, cos, well, it's not as though he sees someone correct him and immediately starts with the ad hominems.

Yeah. Phyti ignores and dismisses explanations and evidence, but he does not pretend that such were not even offered in the first place. So I suppose there's that, at least.